
“The problem is all inside your head”
She said to me
“The answer is easy if you
Take it logically
I’d like to help you in your struggle
To be free
There must be fifty ways
To learn arithmetic” [1]
New Math?
According to the song 50 Ways To Leave Your Lover:
She said, “It grieves me so
To see you in such pain
I wish there was something I could do
To make you smile again” [1]
What brings me, and many math students, pain in our relationship with mathematics?
- A student’s emotional connection to math is heavily influenced by their past experiences. Negative experiences like failing tests or feeling humiliated in math class can lead to long-lasting math anxiety.
- Boredom. The relationship is in a rut and we can’t get out.
- Battle fatigue. Fighting with the teacher because the student does not understand, or refuses to put effort into understanding, the material.
- One too many crises (i.e., math tests).
- Many students feel a sense of anxiety, frustration, or even dread when faced with math problems or concepts. This “math anxiety” can be a significant barrier to learning.
After studying mathematics on my own after many years of neglect, tutoring math, and being a substitute teacher for one school year, I appreciate what is stated on the Outschool website.
“When you look at math curriculum or at explanations of math methods, it may seem like math has changed from what you learned as a kid. Despite what it may look like, math hasn’t really changed, but kids are now tasked with gaining a deeper understanding of why math works. ‘New’ math focuses on children gaining a conceptual understanding of math. Today children must understand why math works and how different areas of math are related. ‘Old’ math focused on procedural understanding, which means understanding how to follow a set of rules or steps, but not knowing why they exist.” [3]
“Ay, there’s the rub.” [3] Should ‘old’ math or ‘new’ math be taught? If both, does order matter? From my experience, and what I have read, both are taught in schools. However, I feel that the rub lies in the way they are taught because students are still confused. (Confusion = Boredom.) I do not believe students understand the relationship between ‘old’ and ‘new’ math.
You just slip out the back, Jack
How do we alleviate the pain of mathematics so students will have a good relationship with mathematics? One way is to only teach the standard algorithm (vertical algorithm). Less confusing than teaching both?

“The standard algorithm (vertical algorithm) is generally a faster method but, unlike the area or grid methods, it does not promote understanding or encourage the development of mathematical thinking. Students rarely understand why they are carrying numbers or what that “placeholder zero” is all about in the second row of calculations. It is best to introduce children to long multiplication with the area method/grid method before using the standard algorithm. The area method also supports the important ability to estimate answers.” [4]
I had one teacher instruct the students to use the Magic Zero when multiplying. Magic Zero!? There is nothing magic about it. Until the teacher brought it up in class, I finally realized that when multiplying by the tens place we need to have a zero because we are multiplying by a two-digit number. This confusion and use of the Magic Zero can be eliminated if we just teach the properties of real numbers, especially the distributive property!
13 × 42 = (3 + 10) × 42 = (3 × 42) + (10 × 42) = 126 + 420 = 546
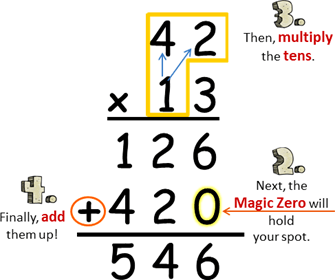
Make a new plan, Stan
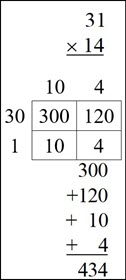
What about using the area (box) method of the ‘new’ math to start with?
“The area method, also sometimes called the box method, is an alternative to the standard algorithmic method for long (multi-digit) multiplication. Both of these methods use the distributive property for multiplication but they differ in how the partial products are calculated and written. The “grid method” is similar to the area method, but it’s not proportional. That is, the grid boxes aren’t drawn to represent the sizes of the parts being multiplied.” [4]
This method allows the teacher to use a visual aid which allows the students to “see” the math, not just memorize procedures. Visuals can: [5]
- Provide concrete models for abstract mathematical concepts
- Help students build intuition and develop deeper understanding
- Facilitate problem-solving by allowing students to visualize relationships and patterns
- Accommodate different learning styles – visual learners in particular benefit from visual aids
- Make math more engaging and accessible, especially for students who struggle with the subject
You don’t need to be coy, Roy
“Just listen to me”
In my experience, the distributive property (and the other properties of real numbers) are either not taught or not emphasized when teaching mathematics. These properties are essential to not only the conceptual understanding, but also the procedural understanding, of mathematics!
I have seen where some teachers and websites use the term partial product multiplication. So I had to research the meaning of that and here is what I found out.
The partial product method is applied to multiply numbers larger than 10.
In this method, we first break the numbers into parts and then multiply the parts.
We add the multiplication results to find the final product.
Let’s call a spade a spade! Partial product multiplication, or method, is just the distributive property! No wonder students are confused. Is math being taught like Dr. Johnson suggests? Using a great many words to teach students mathematics.
“A man who uses a great many words to express his meaning is like a bad marksman who, instead of aiming a single stone at an object, takes up a handful and throws at it in hopes he may hit.” ― Samuel Johnson
Hop on the bus, Gus
“You don’t need to discuss much”
Maybe we should also teach galactic algorithms. 😁 A galactic algorithm is the fastest known way to multiply two numbers, which is based on a 1729-dimensional Fourier transform. [6]

Just drop off the key, Lee

Elizabeth Daniel, a teacher, wrote: “I like to encourage my students to appreciate that there is always more than one way to do every problem, and just because their chosen strategy does not look like mine or someone else’s, does not make their way any better or worse than any other way. We all have to develop our own thinking. I know this may not be seen by some as a positive, you can do it message. But some of my students come to me terrified that they can’t do well in math and that if they don’t do things exactly the same way as I do, then they are wrong. I am trying to give them permission and the confidence to think about math in the way that suits them best.“
“And get yourself free!”
References
[1] “50 Ways To Leave Your Lover.” 2024. The Paul Simon Official Site. Accessed July 1. https://www.paulsimon.com/track/50-ways-to-leave-your-lover/.
[2] “Why ‘new’ Math Isn’t New and Why You Shouldn’t Be Scared of It.” 2024. Outschool. Accessed July 2. https://outschool.com/articles/new-math-isnt-new.
[3] “Hamlet, Act 3, Scene 1 – Video Note: Word Nerd: ‘Rub.’” 2024. myShakespeare. https://myshakespeare.com/hamlet/act-3-scene-1-video-note-word-nerd-rub.
So when Hamlet says “there’s the rub” , he’s saying that the rub, or the obstacle, to our thinking that sleep and death are exactly the same is that we don’t know what dreams are like when we’re dead — this unknown aspect to death is the rub, or the obstacle, to us finding death more appealing.
[4] Zimmerman, Alycia. “A Guide for Parents to Non-Standard Methods for Multi-Digit Multiplication”. 2015. https://www.scholastic.com/content/dam/teachers/blogs/alycia-zimmerman/migrated-files/non-standard_multiplication_methods_parents_letter.pdf.
[5] “Fast, Helpful AI Chat.” 2024. Poe. Assistant. Accessed June 15. https://poe.com/.

I used AI bots in this article to capture ideas that I could not develop on my own without more extensive research. I recall back in the 1990s attending presentations at conferences where the presenter was using crawler bots to gather information for their research. I am still experimenting with AI bots, and will continue to use them as needed to present ideas and concepts more clearly to the reader.
[6] “Galactic Algorithm.” 2024. iFunny. Accessed July 2. https://br.ifunny.co/picture/galactic-algorithm-from-wikipedia-the-free-encyclopedia-a-galactic-algorithm-1FZQ8wJj7.
Additional Reading
Brack, Tyne. 2023. “5 Multiplication Strategies.” Maneuvering the Middle. October 25. https://www.maneuveringthemiddle.com/5-multiplication-strategies/.
Do your students often make mistakes using the standard multiplication algorithm? Then this post is for you! Here are 5 alternative multiplication strategies for your upper elementary and middle school students.
“Different Methods of Multiplication.” 2022. Smartick. May 20. https://www.smartick.com/blog/mathematics/multiplication-and-division/different-methods-multiplication/.
In today’s post we’re going to find out how ancient cultures would have solved the multiplication we’ve chosen. We’re going to look at Chinese and Egyptian methods of multiplication. To help make sure you’ve understood, we’ll demonstrate each method by solving the multiplication 31 x 42 using both.
“Different Ways of Multiplying Numbers: WeTheStudy.” 2024. WeTheStudy. Accessed July 1. https://www.wethestudy.com/feature-posts/different-ways-of-multiplying-numbers.
There are multiple ways to perform multiplication between numbers. In this post, we explore the different techniques to get the product of two numbers.
“Galactic Algorithm.” 2024. Wikipedia. Wikimedia Foundation. June 13. https://en.wikipedia.org/wiki/Galactic_algorithm#Integer_multiplication.
A galactic algorithm is one that runs faster than any other algorithm for problems that are sufficiently large, but where “sufficiently large” is so big that the algorithm is never used in practice. This means it will not reach its stated efficiency until the numbers have (vastly) more digits than there are atoms in the universe. So this algorithm is never used in practice.
Knudson, Kevin, Professor of Mathematics. 2024. “The Common Core Is Today’s New Math – Which Is Actually a Good Thing.” The Conversation. June 25. https://theconversation.com/the-common-core-is-todays-new-math-which-is-actually-a-good-thing-46585.
As an instructor of college-level mathematics, I view this focus on conceptual understanding and multiple strategies for solving problems as a welcome change. Doing things this way can help build intuition about the size of answers and help with estimation. College students can compute answers to homework problems to 10 decimal places, but ask them to ballpark something without a calculator and I get blank stares. Ditto for conceptual understanding – for instance, students can evaluate integrals with relative ease, but building one as a limit of Riemann sums to solve an actual problem is often beyond their reach.
Rebecca T. “I often hear people say, “My math teacher/professor is terrible at explaining.” Why does this seem to happen in math classes much more often than other classes?” 2024. Quora. Accessed June 14. https://qr.ae/psmLva.
Sometimes, you just got to suck it up and do it the way the teacher and the system is asking you to do it. Sometimes, they are asking you to do it a certain way for a reason you won’t understand until later. Usually, the teacher does not choose the method, its a curriculum and system thing. Rarely, is the teacher truly terrible at explaining, but it happens from time to time.
Zeke the Geek. 2024. “It Is Not in Our Stars To Hold Our Mathematical Destiny but Ourselves.” Mathematical Mysteries. June 1. https://mathematicalmysteries.org/2024/06/01/it-is-not-in-our-stars-to-hold-our-mathematical-destiny-but-ourselves/.
