Definition
The Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function’s derivatives at a single point. It is named after the British mathematician Brook Taylor, who introduced the concept in the 18th century. By using a finite number of terms in the series, we can get a good approximation of the original function near a specific point. The more terms we include, the closer the approximation becomes to the actual function.
A Taylor Series simply approximates a function around a point. Basically, you take a point, and use the derivative to figure out how much the function would change if you move away from that point. And then use the second derivative to refine your guess on how much it would move. And the third, and so on until you get accurate enough. A Taylor Series is basically math-speak for just eyeballing it.
This sounds very pointless when we have the function and can just plug in x to get f(x), but more often than not, these functions are so complex, it’s incredibly difficult to calculate it. So, you just approximate it, and your approximation comes out as a neat, clean polynomial. [11]
Who
Taylor series are mostly used in various fields of physics, mathematics, and engineering. They provide a powerful tool for solving differential equations, evaluating limits, and analyzing the behavior of functions. They also form the basis for many numerical methods and algorithms used in scientific computations.
Approximation of Functions
With the help of the Taylor series, we can easily find the approximate solution of complicated functions. By truncating the series to a finite number of terms, we can obtain an approximation of a function around a specific point. This approximation becomes more accurate as we include higher-order terms in the series.
Calculating Derivatives
By using the Taylor series, we can find the derivative of any function. By expressing a function as a Taylor series, we can differentiate the series term by term, which allows us to obtain derivatives of the original function at a given point.
Numerical Analysis
Taylor series plays a fundamental role in numerical methods for solving differential equations, integrals, and optimization problems. Techniques such as Euler’s method, Runge-Kutta method, and Newton’s method rely on Taylor series expansions to approximate solutions and iteratively refine them.
Physics and Engineering
Taylor series is widely used in physics and engineering to simplify complex mathematical models. By approximating nonlinear equations or functions with Taylor series, it becomes easier to analyze and solve problems in fields like mechanics, electromagnetism, thermodynamics, and control systems.
Error Finding
Taylor series provides a framework for finding analysis in arithmetical computations. By comparing the original function to its Taylor series approximation, we can estimate the error introduced by truncating the series. This information is valuable in determining the accuracy and convergence of numerical methods.
Signal Processing
In signal processing, the Taylor series can be used to represent signals as a sum of sine and cosine functions (Fourier series). This decomposition allows the analysis and manipulation of signals in the frequency domain, leading to applications in image processing, audio compression, telecommunications, and more.
Probability and Statistics
Taylor series expansions are used to derive moment-generating functions, which provide a convenient way to study the properties of random variables in probability and statistics. The expansion helps in finding moments, computing probabilities, and approximating distributions.
What
Formula for a Taylor series
The general formula for a Taylor series expansion of a function f(x) centered around a is:
f(x) = f(a) + (x – a) f’(a) + [(x-a)2f’’(a)/2!] + [(x – a)3 f’’’(a)/3!] + …+ [(x-a) f(n)(a)/n!]]
or
f(x) = (x-a) ∑∞n=0 f(n)(a)/n!
- f(a) represents the value of the function at the point a.
- f'(a) represents the first derivative of the function evaluated at a.
- f”(a) represents the second derivative at a.
- n! denotes the factorial of n.
By looking at the localized behavior of a function, we can often gain amazing insights. This is where the Taylor series is really useful. Simply put, the Taylor series is a representation of a function that can help us do mathematics. Uses of the Taylor series include analytic derivations and approximations of functions. [6]
| Function | Taylor Expansion |
|---|---|
| ex at x = 0 | 1 + x + x2 /2! + x3 /3! + x4 /4! + x5/5! + … |
| sin(x) | x – x3/3! + x5/5! – x7/7! + x9/9! – … |
| cos(x) | 1 – x2/2! + x4/4! – x6/6! + x8/8! – … |
| tan(x) | x + x3/3 + 2x5/15 + 17x7/315 + 62x9/2835 + … |
| ln(x) | x – (1/2)x2 + (1/3)x3 + (1/4)x4 + … |
A Taylor series is a mathematical concept found in computer science, calculus, chemistry, physics, and other fields of higher mathematics. A function’s estimate (guess) is created by using a series of operations. Taylor series can also be classified as Maclaurin series with center at 0. [1]
What is the difference between Taylor series and Maclaurin series?
In math, a Taylor Series or Taylor Polynomial consists of an infinite sum of terms calculated from the derivatives of a function at a single point. Maclaurin series is a special case of Taylor series, which have zero as the specific point. [1]
Power Series Centered at x=a.
Power series don’t have to be centered at 0. They can be centered at any point x=a, in which case the series will contain powers of (x−a) instead of powers of x. Since the interval of convergence of a power series has a center that is the x-value where the series is centered, if a power series centered at a has radius of convergence R, its interval of convergence will be from a−R to a+R. All possible intervals of convergence of such a series are: [2]
[a−R, a+R], (a−R, a+R], [a−R, a+R), (a−R, a+R), {a}=[a, a] and (−∞,∞).
Choosing the centre of Taylor series is significant for the accuracy of your approximation for a given number of terms of the series. For example, if you choose a centre of x=0 and you use the Taylor series to evaluate a function when x=20, then you will need to take more terms to obtain a reasonable answer. On the other hand if the centre was at x=18 and you evaluate f(20) then less number of terms would be needed to obtain a reasonable answer.
Summary: for highly accurate answers, try to keep your centre close to the values of x that you want to evaluate. [3]
Taylor Series represents the accumulation of several calculus topics, and I would name it as one of the most significant results in calculus, just behind both fundamental theorems and the mean value theorem. Taylor series can be used to prove a multitude of identities, including the famous Euler’s formula. We can use them to approximate nasty integrals to whatever degree of accuracy we wish. We use them in the study of differential equations to approximate solutions to a given relation.
How awesome is it that you can represent any infinitely-differentiable function as an infinite polynomial? How awesome is it that you can represent these functions in a closed form? Moreover, isn’t it amazing that we can even bound the error on our approximation? Isn’t it particularly wondrous that you can approximate an entire function just by observing its behavior at a single point?
Guess how your calculator computes ex. (The answer is a Taylor polynomial.)
Guess how you find the best-fitting hyperplane to a given function in multivariate calculus. (The answer is a Taylor Polynomial).
Guess what a tangent line is. (The answer is a Taylor Polynomial.)
Guess how you can get around icky integrals and limits. (The answer is a Taylor Polynomial.)
So what is the significance? Any function satisfying a few criteria can be represented as an infinite polynomial. I think that’s pretty significant. [4]
What is the Taylor series for sin (x) centered at pi? [5]
Consider that
sin(x−π) = −sin(x)
Therefore
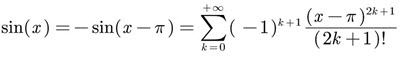
Why
Because they allow us to approximate a function by a polynomial near some point, and polynomials are easy functions to do mathematics with (as compared to n-th roots, trigonometric functions, exponentials, etc.).—polynomials use only arithemetic.
For example, we could estimate (19)1/4 as closely as we’d like by finding a Taylor polynomial of some degree for f(x) = x1/4 centered at a = 16 (where our function and its derivatives are all nice, rational numbers), and plug 19 into the polynomial instead. The higher degree polynomial we take, the better in general our estimate will get, and the Error Theorem lets us determine an upper bound on the error in our estimation. [10]
See Theoretical Knowledge Vs Practical Application.
How
To find the Taylor series of a function, you need to calculate its derivatives at a specific point and use them to construct the series. The general formula for a Taylor series expansion involves evaluating the function and its derivatives at the chosen point, multiplying them by appropriate powers of (x – a), and dividing by the corresponding factorials.
Example 1 – Simple
Find the Taylor series of f(x)= x4+10x3+9x -7 at x = 4
Step 1:
Evaluate the function at x = 4
f(4) = (4)4 + 10(4)3 + 9(4) – 7
f(4) = 256 + 640 +36 – 7
f(4) = 925
Step 2:
Differentiate f(x) with respect to x
f’(x) = 4x3 + 30x2 + 9
then evaluate the first derivative at x = 4
f’(x) = 4(4)3 + 30(4)2 + 9
f’(x) = 256 + 480 +9
f’(x) = 745
Step 3:
Differentiate the first derivative with respect to x
f’’(x) = 12x2 + 60x
Then evaluate the second derivative at x = 4
f’’(x) = 12(4)2 + 60(4)
f’’(x) = 192 + 240
f’’(x) = 432
Step 4:
Differentiate the second derivative with respect to x
f’’’(x) = 24x + 64
Then evaluate the third derivative at x = 4
f’’’(x) = 24(4) + 64
f’’’(x) = 96 + 64
f’’’(x) = 160
Step 5:
Now differentiate the third derivative with respect to x
f’’’’(x) = 24
Evaluate the fourth derivative at x=4
f’’’’(4) = 24
Step 6:
Lastly, differentiate the fourth derivative with respect to x
f’’’’(x) = 24
f’’’’’(x) = 0
Therefore, the required Taylor series is:
f(x) = x4 + 10x3 + 9x – 7 = (x-4)n ∑∞n=0 f(n)(4)/n!
= f(4) + (x-4)f’(4) + (x-4)2f’’(4)/2! + (x-4)3f’’’(4)/3!+ (x-4)4f’’’’(4)/4! + 0
Here we put the value of the required derivative function
= 925 + 745(x-4) + (x-4)2(432/2!) + (x-4)3(160/3!) + (x-4)4(24/4!)
Now simplify the equation to obtain the Taylor series for f(x)= x4+10x3+9x -7 at x = 4
= 925 + 745(x-4) + 216(x-4)2 + 26.67(x-4)3 + (x-4)4
Example 2 – Limit
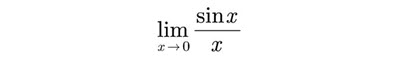
The first thing to notice about this limit is that, as x tends to zero, both the numerator, sin(x), and the denominator, x, tend to 0. So we may not evaluate the limit of the ratio by simply dividing the limits of the numerator and denominator. To find the limit, or show that it does not exist, we are going to have to exhibit a cancellation between the numerator and the denominator. Let’s start by taking a closer look at the numerator.
sin(x) = x – x3/3! + x5/5! – x7/7! + x9/9! – …
Consequently
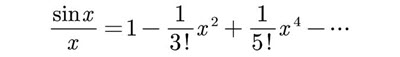
Every term in this series, except for the very first term, is proportional to a strictly positive power of x. Consequently, as x tends to zero, all terms in this series, except for the very first term, tend to zero. In fact the sum of all terms, starting with the second term, also tends to zero. That is,
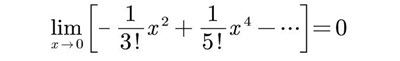
We won’t justify that statement here, but it will be justified in the following (see Optional — The Big O Notation) subsection. So
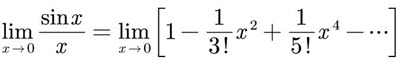
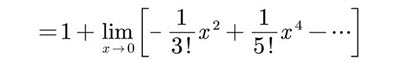
= 1
The limit in the previous example can also be evaluated relatively easily using l’Hôpital’s rule. While the following limit can also, in principal, be evaluated using l’Hôpital’s rule, it is much more efficient to use Taylor series . [7]
See also Example 3.6.23 A not so easy limit made easier.
Example 3 – Differentiation
Example: Estimate the first derivative of
f(x) = −0.1x4 − 0.15x3 − 0.5x2 − 0.25x + 1.2
at x = 0.5 using a step size h = 0.5. Repeat the computation using h = 0.25.
See pages 19-24 of Chapter 5: Numerical Integration and Differentiation, and see Example 8.8.8: Using Taylor series to solve differential equations for additional examples.
Example 4 – Integration
Solving differential equations is one common application of power series. We now turn to a second application. We show how power series can be used to evaluate integrals involving functions whose antiderivatives cannot be expressed using elementary functions.
One integral that arises often in applications in probability theory is ∫e−x^2dx. Unfortunately, the antiderivative of the integrand e−x^2 is not an elementary function. By elementary function, we mean a function that can be written using a finite number of algebraic combinations or compositions of exponential, logarithmic, trigonometric, or power functions. We remark that the term “elementary function” is not synonymous with noncomplicated function. For example, the function f(x) = √(x2−3x) + ex^3− sin(5x+4) is an elementary function, although not a particularly simple-looking function. Any integral of the form ∫f(x)dx where the antiderivative of f cannot be written as an elementary function is considered a non-elementary integral.
Non-elementary integrals cannot be evaluated using the basic integration techniques discussed earlier. One way to evaluate such integrals is by expressing the integrand as a power series and integrating term by term. We demonstrate this technique by considering ∫e−x^2dx. [8]
See Example 11.11.6: Using Taylor Series to Evaluate a Definite Integral
Many of the References and Additional Reading websites and Videos will assist you with understanding and applying Taylor and Maclaurin Series.
As some professors say: “It is intuitively obvious to even the most casual observer.“
References
[1] Darji, Chetan. 2022. “An introduction to Taylor series: Definition, formulas, and calculations”. Stud Mentor – Where Learning Begins. https://www.studmentor.com/an-introduction-to-taylor-series-definition-formulas-and-calculations/.
[2] “Power Series”. 2023. web.ma.utexas.edu. https://web.ma.utexas.edu/users/m408s/m408d/CurrentWeb/LM11-8-6.php.
[3] Mortadha, Jafar. “What is the significance of centering a Taylor Series at some value of x?”. 2023. Quora. https://qr.ae/py9Lal.
[4] Govind, Sachin. “What is really the significance of Taylor’s series?”. 2023. Quora. https://qr.ae/py9LVo.
[5] Everett, Lance. “What is the Taylor series for sin (x) centered at pi?”. 2021. Quora. https://qr.ae/py9Lq4.
[6] “What is the Taylor Series?”. 2023. Study.com. https://study.com/academy/lesson/taylor-series-definition-formula-examples.html.
[7] ⭐ “3.6: Taylor Series – Mathematics LibreTexts”. 2023. Mathematics LibreTexts. https://math.libretexts.org/Bookshelves/Calculus/CLP-2_Integral_Calculus_(Feldman_Rechnitzer_and_Yeager)/03%3A_Sequence_and_series/3.06%3A_Taylor_Series.
[8] “11.11: Applications Of Taylor Polynomials”. 2017. Mathematics LibreTexts. https://math.libretexts.org/Bookshelves/Calculus/Map%3A_Calculus__Early_Transcendentals_(Stewart)/11%3A_Infinite_Sequences_And_Series/11.11%3A_Applications_of_Taylor_Polynomials.
[9] “Chapter 5: Numerical Integration and Differentiation”. 2023. ece.mcmaster.ca. https://www.ece.mcmaster.ca/~xwu/part6.pdf.
[10] Swenton, Frank. “Why are we using Taylor and Maclaurin series?”. 2019. Quora. https://qr.ae/pyiqIU.
[11] Trivedi, Noel. “What Is The Taylor Series, Exactly?”. 2023. Quora. https://qr.ae/pyi06n.
Additional Reading
“2.02: Numerical Differentiation Of Continuous Functions”. 2023. Mathematics LibreTexts. https://math.libretexts.org/Under_Construction/Numerical_Methods_with_Applications/2%3A_Differentiation/2.02%3A_Numerical_Differentiation_of_Continuous_Functions.
After successful completion of this lesson, you should be able to: 1) derive formulas for approximating the first derivative of a function, 2) use the developed formulas in examples to estimate derivatives of a function.
“6: Finite Difference Approximation – Mathematics LibreTexts”. 2023. Mathematics LibreTexts. https://math.libretexts.org/Bookshelves/Scientific_Computing_Simulations_and_Modeling/Scientific_Computing_(Chasnov)/I%3A_Numerical_Methods/6%3A_Finite_Difference_Approximation.
We introduce here numerical differentiation, also called finite difference approximation. This technique is commonly used to discretize and solve partial differential equations.
“6.3 Taylor and Maclaurin Series – Calculus Volume 2 | openstax”. 2023. openstax.org. https://openstax.org/books/calculus-volume-2/pages/6-3-taylor-and-maclaurin-series.
“6.4 Working With Taylor Series – Calculus Volume 2 | openstax”. “Taylor’s Theorem with Remainder”. 2023. openstax.org. https://openstax.org/books/calculus-volume-2/pages/6-4-working-with-taylor-series.
“8.4: Taylor Series Examples”. 2017. Mathematics LibreTexts. https://math.libretexts.org/Bookshelves/Analysis/Complex_Variables_with_Applications_(Orloff)/08%3A_Taylor_and_Laurent_Series/8.04%3A_Taylor_Series_Examples.
The uniqueness of Taylor series along with the fact that they converge on any disk around z0 where the function is analytic allows us to use lots of computational tricks to find the series and be sure that it converges.
“8.8: Taylor Series”. 2017. Mathematics LibreTexts. https://math.libretexts.org/Bookshelves/Calculus/Calculus_3e_(Apex)/08%3A_Sequences_and_Series/8.08%3A_Taylor_Series.
In Section 8.6, we showed how certain functions can be represented by a power series function. In Section 8.7, we showed how we can approximate functions with polynomials, given that enough derivative information is available. In this section we combine these concepts: if a function f(x) is infinitely differentiable, we show how to represent it with a power series function.
“10.1: Power Series And Functions”. 2016. Mathematics LibreTexts. https://math.libretexts.org/Bookshelves/Calculus/Calculus_(OpenStax)/10%3A_Power_Series/10.01%3A_Power_Series_and_Functions.
A power series is a type of series with terms involving a variable. More specifically, if the variable is x, then all the terms of the series involve powers of x. As a result, a power series can be thought of as an infinite polynomial. Power series are used to represent common functions and also to define new functions. In this section we define power series and show how to determine when a power series converges and when it diverges. We also show how to represent certain functions using power series.
“10.3E: Exercises For Taylor Polynomials And Taylor Series”. 2019. Mathematics LibreTexts. https://math.libretexts.org/Courses/Monroe_Community_College/MTH_211_Calculus_II/Chapter_Ch10%3A_Power_Series/10.3%3A_Taylor_and_Maclaurin_Series/10.3E%3A_Exercises_for_Taylor_Polynomials_and_Taylor_Series.
“Calculus II – Power Series”. 2023. tutorial.math.lamar.edu. https://tutorial.math.lamar.edu/classes/calcii/powerseries.aspx.
We’ve spent quite a bit of time talking about series now and with only a couple of exceptions we’ve spent most of that time talking about how to determine if a series will converge or not. It’s now time to start looking at some specific kinds of series and we’ll eventually reach the point where we can talk about a couple of applications of series. In this section we are going to start talking about power series. A power series about a, or just power series, is any series that can be written in the form,

where a and cn are numbers. The cn’s are often called the coefficients of the series. The first thing to notice about a power series is that it is a function of x. That is different from any other kind of series that we’ve looked at to this point. In all the prior sections we’ve only allowed numbers in the series and now we are allowing variables to be in the series as well. This will not change how things work however. Everything that we know about series still holds.
“Calculus II – Taylor Series (Practice Problems)”. 2023. tutorial.math.lamar.edu. https://tutorial.math.lamar.edu/Problems/CalcII/TaylorSeries.aspx.
“Examples of limits that become easier with Taylor series”. 2017. math.stackexchange.com. https://math.stackexchange.com/questions/1904644/examples-of-limits-that-become-easier-with-taylor-series.
“Introduction to Numerical Methods/Numerical Differentiation – Wikibooks”. 2023. en.wikibooks.org. https://en.wikibooks.org/wiki/Introduction_to_Numerical_Methods/Numerical_Differentiation.
 Merriam, Areeba. 2023. “History of the Taylor Series.” Medium. Cantor’s Paradise. October 1. https://www.cantorsparadise.com/history-of-the-taylor-series-dc173b5836fe.
Merriam, Areeba. 2023. “History of the Taylor Series.” Medium. Cantor’s Paradise. October 1. https://www.cantorsparadise.com/history-of-the-taylor-series-dc173b5836fe.
⭐ Padhi, Vedant. 2025. “Taylor’s Series (and It’s Friend, Maclaurin).” Medium. Medium. April 13. https://medium.com/@vedantpadhiii/taylors-series-and-it-s-friend-maclaurin-45e3dcd4057a.
More surprising, however, was learning that these ideas — developed centuries ago — still power modern applications from computer algorithms to orbital mechanics. The story of Taylor and Maclaurin Series is as much about the history of mathematical concepts as about calculation. The general Taylor Series formula was introduced formally by the English mathematician Brook Taylor in 1715 in his publication Methodus Incrementorum Directa et Inversa. Taylor was trying to find out how functions change, and he realized that derivatives — rates of change — could be used recursively to approximate nearly any smooth function locally. A few decades later, the Scottish mathematician Colin Maclaurin built on Taylor’s work with a focus on expansions about zero.
“Taylor Series”. 2023. mathsisfun.com. https://www.mathsisfun.com/algebra/taylor-series.html.
“Taylor Series (Proof And Examples)”. 2023. BYJU’S. https://byjus.com/maths/taylor-series/.
“Taylor Series: Formula, Proof, Examples, And FAQs”. 2020. GeeksForGeeks. https://www.geeksforgeeks.org/taylor-series/.
“Taylor Series: Formula, Theorem with Proof Method with Examples”. 2023. testbook.com. https://testbook.com/maths/taylor-series.
“Taylor Series Calculator – Find Taylor Expansion With Steps”. 2023. limitcalculator.online. https://www.limitcalculator.online/taylor-series-calculator.
“Where do Taylor Series come from and why do we learn about them?”. 2023. blog.cambridgecoaching.com. https://blog.cambridgecoaching.com/where-do-taylor-series-come-from-and-why-do-we-learn-about-them.
We started at linear approximations, moved on to polynomial approximations, and ended on Taylor series, which are in a way infinitely good polynomial approximations. Whenever we want to approximate a complicated function numerically, we can take the first few terms of the Taylor series expansion of the function to get a nice polynomial approximation. The more terms we take, the better approximation we get. This relationship to polynomial approximations is just one of the many properties of Taylor series that make them such a useful and powerful mathematical tool!
Videos
This calculus 2 video tutorial explains how to find the Taylor series and the Maclaurin series of a function using a simple formula. It explains how to derive power series of composite functions using known Maclaurin series of elementary functions. This tutorial has a ton of examples and practice problems.
This calculus 2 video tutorial provides a basic introduction into Taylor Polynomials and Maclaurin Polynomials. It explains how to find the 4th degree polynomial approximation of lnx and ex. A Maclaurin polynomial approximation can be found using a Taylor Polynomial approximation centered at 0. This video contains a few examples and practice problems.
Taylor series is a great way to approximate functions with polynomials. The more you know about the derivatives of the function at x=a, the better an approximation you will get.
Power series don’t have to be powers of x. They can be powers of (x-a). In that case, the interval of convergence is an interval of radius R, centered at a.
This calculus 2 video tutorial provides a basic introduction into the representation of functions as power series. It explains how to represent a function as a power series centered at 0 and centered at some value c. It also explains how to approximate function values using geometric power series. This video also explains how to find the radius of convergence and the interval of convergence of a geometric power series. To write a power series from a function, you need to write the function in the form of the formula for the infinite sum of a geometric series. To find the interval of convergence, find the common ratio represented by some variable expression of x and set it less than 1 and solve the inequality. This video also includes examples and practice problems of adding and subtracting power series as well as using partial fraction decomposition.
This calculus video tutorial provides a basic introduction into power series. it explains how to find the radius of convergence and the interval of convergence of a power series using the ratio test. If the limit of the ratio test is zero, the power series converges for all x values. If the limit is infinity, the power series converges only when x equals c such that the power series is centered at c. If the limit equals an absolute value expression based on x, the interval of convergence will have a finite range. This video provides a plot of the interval of convergence on a number line so you can see how it relates to the radius of convergence. In addition, you must check the endpoints for the interval of convergence using the original power series expressed in sigma notation. This video contains plenty of examples and practice problems,
⭐ I suggest that you read the entire reference. Other references can be read in their entirety but I leave that up to you.
 Medium Member Only
Medium Member Only
The featured image on this page is from the Cambridge Coaching website.
