Definition
The slope of a line is the measure of the steepness and the direction of the line. Finding the slope of lines in a coordinate plane can help in predicting whether the lines are parallel, perpendicular, or none without actually using a compass.
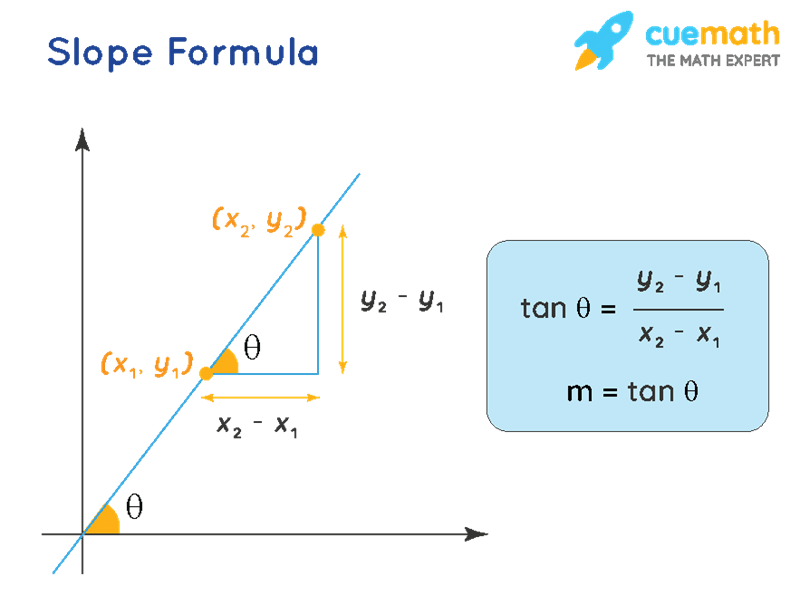
The slope of any line can be calculated using any two distinct points lying on the line. The slope of a line formula calculates the ratio of the “vertical change” to the “horizontal change” between two distinct points on a line. In this article, we will understand the method to find the slope and its applications. [1]
Who
Occupations that are concerned with slope include:
- Civil Engineers: Civil engineers design and oversee the construction of infrastructure projects, such as roads, bridges, and buildings. Understanding slope is critical in their work, as it affects factors like drainage, stability, and accessibility.
- Surveyors: Surveyors use various instruments and techniques to measure and map the terrain, including the slopes of the land. This information is crucial for construction projects, land use planning, and other applications.
- Landscape Architects: Landscape architects design outdoor spaces, such as parks, gardens, and public areas. They need to understand slope to ensure proper drainage, accessibility, and aesthetic considerations.
- Urban Planners: Urban planners are responsible for the development and management of cities and communities. Slope is an important factor in their planning decisions, affecting infrastructure, transportation, and land use.
- Construction Workers: Construction workers, such as excavators, graders, and pavers, need to understand slope to ensure the stability and safety of the structures they are building.
- Geologists: Geologists study the Earth’s physical structure and substance, including the slope and topography of the land. This information is important for activities like mining, resource extraction, and natural hazard assessment.
- Hydrologists: Hydrologists study the movement, distribution, and quality of water, including how water flows across different slopes and terrain.
- Agricultural Engineers: Agricultural engineers design and develop systems for crop production, irrigation, and land management. Understanding slope is crucial for their work, as it affects soil erosion, irrigation, and the placement of farm equipment.
Understanding and properly accounting for slope is important in a wide range of professions that deal with the built and natural environment. [3]
What
The slope of a line is defined as the change in y coordinate with respect to the change in x coordinate of that line. The net change in y coordinate is Δy, while the net change in the x coordinate is Δx. So the change in y coordinate with respect to the change in x coordinate can be written as,
m = Δy/Δx
where, m is the slope
Note that tan θ = Δy/Δx
We also refer this tan θ to be the slope of the line. [1]

1 — Positive Slope : A positive slope indicates that as the independent variable x increases, the dependent variable y also increases as we saw in the examples above.
2 — Negative Slope : Indicates that as the independent variable x increases, the dependent variable y decreases.
3 — Zero Slope : A zero slope indicates that the dependent variable y does not change as the independent variable x increases, resulting in a horizontal line.
4 — Undefined Slope : An undefined slope occurs when the line is vertical, meaning the independent variable x remains constant while the dependent variable y changes. [2]
Why
The concept of slope is fundamental to understanding the core ideas and applications of calculus, as it provides the geometric interpretation and the basis for many of the key concepts and techniques in this field of mathematics. [3]
Derivative and Tangent Lines
The derivative in calculus is defined as the slope of the tangent line to a function at a given point. Understanding the concept of slope is crucial for interpreting the derivative and its geometric interpretation as the rate of change of the function.
Rates of Change
Calculus is the study of rates of change, and slope represents the rate of change of a function at a specific point. The derivative, which is the fundamental concept in calculus, measures the instantaneous rate of change of a function.
Optimization Problems
Many optimization problems in calculus involve finding the maximum or minimum values of a function. These problems often require finding the points where the slope of the function is zero, as these points represent the critical points of the function.
Differentiation and Integration
The process of differentiation, which involves finding the derivative of a function, relies heavily on the concept of slope. Conversely, the process of integration, which is the inverse of differentiation, can be interpreted as finding the area under a curve, which is related to the accumulation of the function’s slope over an interval.
Applications of Calculus
Many real-world applications of calculus, such as in physics, engineering, and economics, involve understanding the rates of change and the relationship between a function and its slope. Mastering the concept of slope is essential for applying calculus principles in these domains.
See Theoretical Knowledge Vs Practical Application.
How
Many of the References and Additional Reading websites and Videos will assist you with understanding and applying slope.
As some professors say: “It is intuitively obvious to even the most casual observer.“
References
[1] “Slope – Definition, Types, Examples: Slope of Line Formula.” 2024. CUEMATH. Accessed August 5. https://www.cuemath.com/geometry/slope/.
[2]  Soula, Dr. Walid. 2024. “Introduction to Slope.” Medium. Medium. August 5. https://medium.com/@soulawalid/introduction-to-slope-1a9859706788.
Soula, Dr. Walid. 2024. “Introduction to Slope.” Medium. Medium. August 5. https://medium.com/@soulawalid/introduction-to-slope-1a9859706788.
[3] “Fast, Helpful AI Chat.” 2024. Poe. Assistant. Accessed August 5. https://poe.com/.

I used AI bots in this article to capture ideas that I could not develop on my own without more extensive research. I recall back in the 1990s attending presentations at conferences where the presenter was using crawler bots to gather information for their research. I am still experimenting with AI bots, and will continue to use them as needed to present ideas and concepts more clearly to the reader.
Additional Reading
“Slope Formula – What Is Slope Formula? Equation, Examples.” 2024. CUEMATH. Accessed August 5. https://www.cuemath.com/slope-formula/.
“Slope Formula – What Is Slope Formula? Equation, Examples, FAQs.” 2024. GeeksforGeeks. GeeksforGeeks. May 7. https://www.geeksforgeeks.org/slope-formula/?ref=gcse.
“Undefined Slope: Definition, Equation, Meaning, Graph & Examples.” 2023. GeeksforGeeks. GeeksforGeeks. November 30. https://www.geeksforgeeks.org/undefined-slope/?ref=gcse.
“Slope Intercept Form of Line: Formula, Derivation and Examples.” 2024. GeeksforGeeks. GeeksforGeeks. June 20. https://www.geeksforgeeks.org/slope-intercept-form/?ref=gcse.
“Slope of a Line: Definition, Types, Formulas, Examples, and FAQs.” 2024. GeeksforGeeks. GeeksforGeeks. May 7. https://www.geeksforgeeks.org/slope-of-line/?ref=gcse.
“Point Slope Form Formula of a Line.” 2024. GeeksforGeeks. GeeksforGeeks. https://www.geeksforgeeks.org/point-slope-form-formula-of-a-line/?ref=gcse.
Videos
This algebra video explains how to find the slope of a line using the rise over run method and by using the formula given two points on the line. This video also discusses how to calculate the slope of a horizontal and a vertical line.
This algebra video tutorial explains how to find the slope of a line given two points and from an equation. It contains examples and practice problems with fractions as well. This video also contains an example of solving for the x and y variable given the slope of a line that passes through a pair of points where you to solve for the missing coordinate.
This algebra video tutorial provides a basic introduction into the slope formula. It also explains how to use it to calculate the slope of the line that passes through two points.
This algebra video provides a basic introduction into vertical lines and their undefined slopes. The slope of a horizontal line, on the other hand, is zero.
This algebra video explains how to write a linear equation in slope intercept form y=mx+b. It also explains how to identify the slope and y-intercept from the equation as well as how to graph the linear equation.
This algebra video tutorial explains how to convert from slope-intercept form to standard form. It also includes linear equations with fractions with examples of two fractions where you need to find the common denominator.
This video explains how to find the x and y intercepts of a line, an equation, and a quadratic function.
This algebra video tutorial provides a basic introduction into point-slope form. It explains how to write a linear equation given a point and the slope. It also explains how to write a linear equation given two points. Finally, it discusses how to graph a linear equation in point-slope form.
⭐ I suggest that you read the entire reference. Other references can be read in their entirety but I leave that up to you.
 Medium Member Only
Medium Member Only
The featured image on this page is from the CUEMATH website.