Definition
Set
A set is an unordered collection of different elements. A set can be written explicitly by listing its elements using set bracket, i.e., { }. If the order of the elements is changed or any element of a set is repeated, it does not make any changes in the set. [1]
Some example of sets:
- Set of all positive integers, I = {1,2,3,4,5,6,7, …}
- A set of all the planets in the solar system P = {Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune}
- Set of vowels in English alphabet, A={a,e,i,o,u}
- Set of odd numbers less than 10, B={1,3,5,7,9}
Set Theory
Set Theory is a branch of mathematical logic where we learn sets and their properties. A set is a collection of objects or groups of objects. These objects are often called elements or members of a set. For example, a group of players in a cricket team is a set. [4]
Set Theory is a branch of Mathematics that studies the collection of objects and operations based on it. Sets are studied under the mathematical logic division of mathematics. A set is simply a collection of objects. The words collection, aggregate, and class are synonymous. On the other hand element, members, and objects are synonymous and stand for the members of the set of which the set is comprised. In this article on Set Theory, we will learn about sets, types of sets, representation of sets, operations on sets, and application of sets in detail. [5]
Who
Have you ever wondered why you learned about sets? They are used everywhere and understanding them is essential to many fields, e.g., mathematics and database programming.
What
German mathematician G. Cantor introduced the concept of sets. He had defined a set as a collection of definite and distinguishable objects selected by the means of certain rules or description. Set theory forms the basis of several other fields of study like counting theory, relations, graph theory and finite state machines. [1]
Why
Set theory is used throughout mathematics. It is used as a foundation for many subfields of mathematics. In the areas pertaining to statistics, it is particularly used in probability. Much of the concepts in probability are derived from the consequences of set theory. Indeed, one way to state the axioms of probability involves set theory. [2]
Database programming. In fact, as a programmer, I use mathematical containers a lot. Bags, Sets, Mappings, Queues, Stacks, etc.
Sets are mathematically the smallest (simplest) container-like structure I know that can be used to describe everything I do for proof purposes (as most mathematicians will find). They are not an end-all-be-all (I find Types to be closer, but still lacking); however, sets are useful whenever I need to work with a situation that asks a question: “Is this included or not?”.
Furthermore, sets and set theory are really a starting point to proof-based math, and more specifically, understanding set theory is a foundation to combinatorics, which is a foundation to probability theory, which is a foundation to statistics.
Therefore, for most people who use statistics, the real life application of set theory is to prepare them for statistical analysis. Of course statistics works on huge collections of data, and you cannot understand the data without understanding the collections.
In general though, most mathematical fields have been built up from set theory first. That includes building up proofs as to why addition of numbers is commutative and associative, etc.
Nicholas Cooper [3]
Set Theory is the foundation of many aspects of Computer Systems Engineering and data management.
- Binary Logic gates used to build microchips in ever digital device.
- ‘Selection’ one of the three fundamental constructs of Programming (the other two being sequence & iteration).
- Sets form the basis of many data structure used in programming, e.g. Set (Java Platform SE 7).
- Databases, Set Theory determines which data will be included and exclude in searches and selections.
- Security & Access control lists for users and systems.
- Distribution lists for messages such as email.
- Cryptography for secure communications.
- Bayesian filtering of junk email.
- Artificial Intelligence decision making.
- Image Recognition.
- Linguistics, Translation and proto-language study.
Martin Spamer, BSc Computer Science & Software Engineering, Staffordshire University [3]
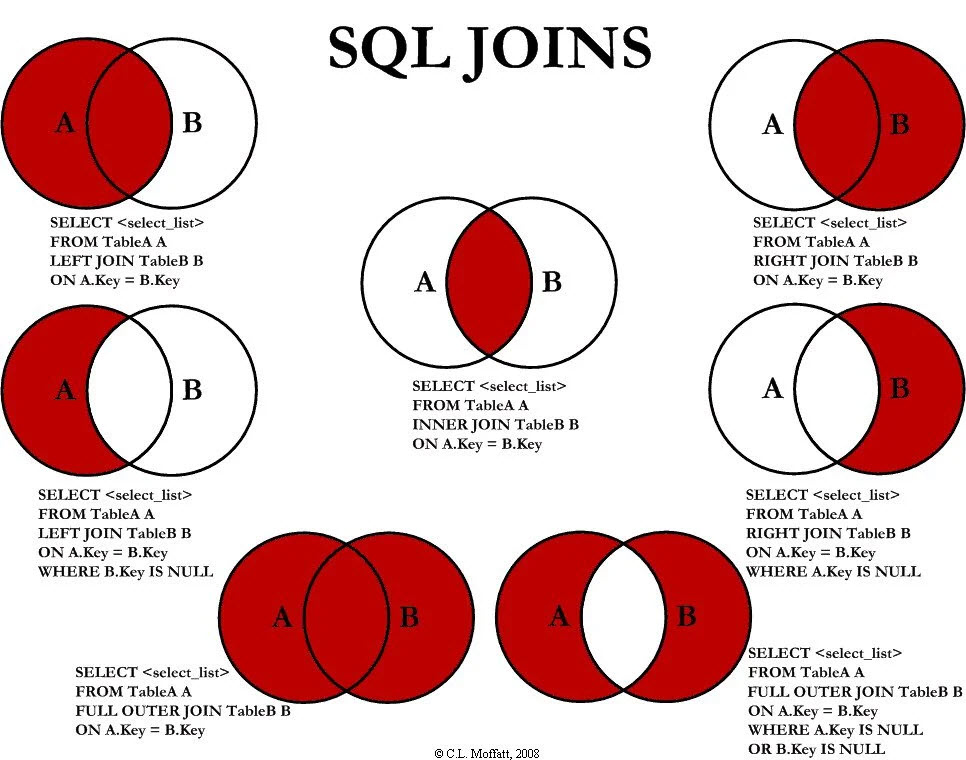
See Theoretical Knowledge Vs Practical Application.
How
Some standard sets used in set theory: [5]
- Set of Natural Numbers is denoted by ℕ
- Set of Whole Numbers is denoted by 𝕎
- Set of Integers is denoted by ℤ
- Set of Rational Numbers is denoted by ℚ
- Set of Irrational Numbers is denoted by 𝕋
- Set of Real Numbers is denoted by ℝ
Many of the References and Additional Reading websites and Videos will assist you with sets & set theory.
As some professors say: “It is intuitively obvious to even the most casual observer.”
References
[1] “Discrete Mathematics – Sets”. 2021. tutorialspoint.com. https://www.tutorialspoint.com/discrete_mathematics/discrete_mathematics_sets.htm.
[2] “The Fundamental Cioncept Of Set Theory”. 2021. thoughtco. https://www.thoughtco.com/what-is-set-theory-3126577.
[3] “What Are Some Real-Life Applications Of Set Theory?”. 2021. Quora. https://www.quora.com/What-are-some-real-life-applications-of-set-theory.
[4] “Set Theory (Basics, Definitions, Types Of Sets, Symbols & Examples)”. 2023. BYJUS. https://byjus.com/maths/basics-set-theory/.
[5] ⭐ “Mathematics | Introduction Of Set Theory – GeeksForGeeks”. 2015. GeeksForGeeks. https://www.geeksforgeeks.org/set-theory/.
Additional Reading
Doerr, Al and Ken Levasseur. “4.2: Laws of Set Theory”. 2023. LibreTexts. https://math.libretexts.org/Bookshelves/Combinatorics_and_Discrete_Mathematics/Applied_Discrete_Structures_(Doerr_and_Levasseur)/04%3A_More_on_Sets/4.02%3A_Laws_of_Set_Theory.
Dutra, Gabriel Macedo. “Understanding Set Theory: A Comprehensive Guide To Mathematical Concepts”. 2023. Medium. https://medium.com/@gabriel.macedo.brother/understanding-set-theory-a-comprehensive-guide-to-mathematical-concepts-c6bf1c153457.
In the realm of mathematics, the theory of sets stands as a foundational framework capable of organizing diverse elements into meaningful groupings. Whether these elements are numbers, individuals, or even fruits, set theory provides a powerful tool to define and categorize them. At its core, the theory assigns lowercase letters to individual elements, designating them as components of a set. For instance, an element “a” or a person “x” can be part of a set. In contrast, sets themselves are represented by uppercase letters enclosed in curly braces ({ }). To enhance clarity, elements within sets are separated by commas or semicolons. Consider the set A = {a, e, i, o, u}.
Falcão, João Renato. “Set Theory — From Pure Math To SQL”. 2022. Medium. https://falcaojoaorenato.medium.com/math-concepts-for-sql-programming-232cb1da0d16.
This article intends to explain the fundamental theory applied in SQL, probability and statistics.
“FREE Step-By-Step Types Of Sets Lesson With Interactive Exercises | Math Goodies”. 2021. mathgoodies.com. https://www.mathgoodies.com/lessons/sets/types-of-sets.
“Introduction To Sets”. 2021. mathsisfun.com. https://www.mathsisfun.com/sets/sets-introduction.html.
“Math: Sets & Set Theory (Video Lessons, Examples And Solutions)”. 2021. onlinemathlearning.com. https://www.onlinemathlearning.com/math-sets.html.
“Probability | Statistics And Probability | Math | Khan Academy”. 2021. Khan Academy. https://www.khanacademy.org/math/statistics-probability/probability-library#basic-set-ops.
“Set (Mathematics) – Wikipedia”. 2021. en.wikipedia.org. https://en.wikipedia.org/wiki/Set_(mathematics).
“Set — From Wolfram MathWorld”. 2021. mathworld.wolfram.com. https://mathworld.wolfram.com/Set.html.
“Set Symbols”. 2021. mathsisfun.com. https://www.mathsisfun.com/sets/symbols.html.
“Set Theory | Basic Concepts Of Set Theory”. 2023. hitbullseye.com. https://www.hitbullseye.com/Quant/Set-Theory.php.
“Set Theory | Introduction To College Mathematics”. 2021. courses.lumenlearning.com. https://courses.lumenlearning.com/atd-hostos-introcollegemath/chapter/set-theory/.
“Sets & Set Theory”. 2021. storyofmathematics.com. https://www.storyofmathematics.com/sets-set-theory.
Students are usually introduced to the concept of sets and set theory at a relatively young age. This introduction, however, may not happen in a math class or be introduced as a separate branch of mathematics. In fact, most people probably first encountered set theory through Venn diagrams of some sort.
⭐ “Set Theory – Definition and Examples”. 2023. storyofmathematics.com. https://www.storyofmathematics.com/set-theory/.
Set theory is a branch of mathematical logic that studies sets, their operations, and properties.
Georg Cantor first initiated the theory in the 1870s through a paper titled “On a property of the collection of all real algebraic numbers.” Through his power set operations, he proved that some infinities are larger than other infinities. This led to the widespread use of Cantorian concepts.
Set theory is one of the foundations of mathematics. It is now considered an independent mathematics branch with applications in topology, abstract algebra, and discrete mathematics.
The following topics are covered in this article: set theory basics, proofs, formulas, and notations.
“Types Of A Set”. 2021. tutorialspoint.com. https://www.tutorialspoint.com/types-of-a-set.
Weiss, Gideon. “An Introduction To Set Theory”. 2023. Medium. https://gidigumdrop.medium.com/an-introduction-to-set-theory-e7f6c6149fd6.
Set theory is a branch of mathematics that deals with collections of objects. Set theory mainly deals with, you guessed it, sets! So… what actually is a set? A set is just a well-defined collection of objects, denoted by curly braces {}. The key word here being “well-defined” meaning there can be no duplicates.
Videos
This video explains “Introduction to Set Theory and Representation of a Set”. Watch the full video for complete explanation.
An explanation of the branch of logic known as set theory which deals with groups of objects and serves as the foundations of mathematics. This series covers the basics of set theory and higher order logic. In this month we are looking at the properties of sets and classes, including transitive sets, swelled sets, supercomplete sets, ordinary sets, proper subsets, null sets, empty sets, universal sets, and void sets. We are also looking at the first four axioms of a basic universe, following Neumann Berneays Gödel (NBG) set theory.
⭐ I suggest that you read the entire reference. Other references can be read in their entirety but I leave that up to you.
The featured image on this page is from the Tuition With Jason website.
