Definition
In mathematics, a series is, roughly speaking, the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures (such as in combinatorics) through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance. [1]
Who
The knowledge of the series is a significant part of calculus and its generalization as well as mathematical analysis. Apart from these applications in mathematics, infinite series are also extensively used in different quantitative disciplines such as statistics, physics, computer science, finance, etc. [XXX]
What
Types of Sequences
Some of the most common examples of sequences are:
Types of Series
Some of the most common examples of series are:
Arithmetic Series
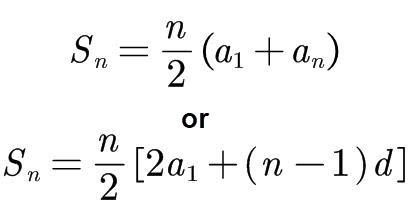
Geometric Series

And the Taylor and Maclaurin series.
Why
See Theoretical Knowledge Vs Practical Application.
How
Many of the References and Additional Reading websites and Videos will assist you with understanding and applying mathematical series.
As some professors say: “It is intuitively obvious to even the most casual observer.“
References
[1] “Series (Mathematics) – Wikipedia”. 2023. en.wikipedia.org. https://en.wikipedia.org/wiki/Series_(mathematics).
[2] “Series (Mathematics) – Definition Of Series, Finite And Infinite Series”. 2023. BYJUS. https://byjus.com/maths/series/.
Additional Reading
“List of Mathematical Series – Wikipedia”. 2023. en.wikipedia.org. https://en.wikipedia.org/wiki/List_of_mathematical_series.
“Mathematical Series (You Should Know)”. 2023. cis.rit.edu. https://www.cis.rit.edu/class/simg716/series_you_should_know.pdf.
Mathematical series representations are very useful tools for describing images or for solving/approximating the solutions to imaging problems. The may be used to “expand” a function into terms that are individual monomial expressions (i.e., “powers”) of the coordinate
MATHS.AI. “Sequences And Series: Comprehensive Mathematical Handbook”. 2023. Medium. https://medium.com/@seoformathsai/sequences-and-series-comprehensive-mathematical-handbook-5863c8f60f17.
Sequences and series are fundamental concepts in mathematics that are used in various fields, from calculus and algebra to number theory and statistics. Understanding these concepts is crucial for solving mathematical problems and real-world applications. In this comprehensive guide, we will delve into the world of sequences and series, providing explanations, examples, and methods to help you grasp these concepts thoroughly.
“Sequence and Series – Difference, Definitions, Examples”. 2023. CUEMATH. https://www.cuemath.com/numbers/sequence-and-series/.
Sequence and series are used in mathematics as well as in our daily lives. A sequence is also known as progression and a series is developed by sequence. Sequence and series is one of the basic concepts in Arithmetic. Sequences are the grouped arrangement of numbers orderly and according to some specific rules, whereas a series is the sum of the elements in the sequence. For example, 2, 4, 6, 8 is a sequence with four elements and the corresponding series will be 2 + 4 + 6+ 8, where the sum of the series or value of the series will be 20.
“Sequence and Series-Definition, Types, Formulas and Examples”. 2023. BYJUS. https://byjus.com/maths/sequence-and-series/.
Sequence and series are the basic topics in Arithmetic. An itemized collection of elements in which repetitions of any sort are allowed is known as a sequence, whereas a series is the sum of all elements. An arithmetic progression is one of the common examples of sequence and series.
– In short, a sequence is a list of items/objects which have been arranged in a sequential way.
– A series can be highly generalized as the sum of all the terms in a sequence. However, there has to be a definite relationship between all the terms of the sequence.
“Sequences and Series: Terminology and Notation”. 2023. purplemath.com. https://www.purplemath.com/modules/series.htm.
A “sequence” (called a “progression” in British English) is an ordered list of numbers; the numbers in this ordered list are called the “elements” or the “terms” of the sequence.
A “series” is what you get when you add up all the terms of a sequence; the addition, and also the resulting value, are called the “sum” or the “summation”. For instance, “1, 2, 3, 4” is a sequence, with terms “1”, “2”, “3”, and “4”; the corresponding series is the sum “1 + 2 + 3 + 4”, and the value of the series is 10.
A sequence may be named or referred to by an upper-case letter such as “A” or “S”. The terms of a sequence are usually named something like “ai” or “an“, with the subscripted letter “i” or “n” being the “index” or the counter. So the second term of a sequnce might be named “a2” (pronounced “ay-sub-two”), and “a12” would designate the twelfth term.
Videos
This calculus 2 video tutorial provides a basic introduction into series. It explains how to determine the convergence and divergence of a series. It explains the difference between a sequence and a series. This video includes examples and practice problems with geometric series, harmonic series, and the telescoping series. It also discusses the divergence test.
This pre-algebra video tutorial explains how to find the next term in a number series. It provides plenty of examples of finding patterns in arithmetic and geometric sequences. This lesson contains tons of number series reasoning tricks including fractions, addition and subtraction series, power series, and more. It explains how to find the common difference of an arithmetic sequence and the common ratio of a geometric sequence.
⭐ I suggest that you read the entire reference. Other references can be read in their entirety but I leave that up to you.
The featured image on this page is from the Series, Summation and Sequences web page on the onlinemathlearning.com website.
