Described as beautiful, elusive and enigmatic, Pi (π) has fascinated and inspired mathematicians throughout history. Deceptively simple, Pi is the ratio of the circumference of a circle to its diameter, calculated by dividing the length of the diameter of a circle into its circumference. The miraculous fact about Pi is that no matter the size of the circle, the value does not change, making Pi a mathematical constant. Adding to its allure, Pi is also an irrational number with no end and no repeating digits. [1]
A Brief History of Pi (π)
Pi (π) has been known for almost 4000 years—but even if we calculated the number of seconds in those 4000 years and calculated π to that number of places, we would still only be approximating its actual value. Here’s a brief history of finding π.
The ancient Babylonians calculated the area of a circle by taking 3 times the square of its radius, which gave a value of pi = 3. One Babylonian tablet (ca. 1900–1680 BC) indicates a value of 3.125 for π, which is a closer approximation.
The Rhind Papyrus (ca.1650 BC) gives us insight into the mathematics of ancient Egypt. The Egyptians calculated the area of a circle by a formula that gave the approximate value of 3.1605 for π.
The first calculation of π was done by Archimedes of Syracuse (287–212 BC), one of the greatest mathematicians of the ancient world. Archimedes approximated the area of a circle by using the Pythagorean Theorem to find the areas of two regular polygons: the polygon inscribed within the circle and the polygon within which the circle was circumscribed. Since the actual area of the circle lies between the areas of the inscribed and circumscribed polygons, the areas of the polygons gave upper and lower bounds for the area of the circle. Archimedes knew that he had not found the value of π but only an approximation within those limits. In this way, Archimedes showed that π is between 3 1/7 and 3 10/71.
A similar approach was used by Zu Chongzhi (429–501), a brilliant Chinese mathematician and astronomer. Zu Chongzhi would not have been familiar with Archimedes’ method—but because his book has been lost, little is known of his work. He calculated the value of the ratio of the circumference of a circle to its diameter to be 355/113. To compute this accuracy for π, he must have started with an inscribed regular 24,576-gon and performed lengthy calculations involving hundreds of square roots carried out to 9 decimal places.
Mathematicians began using the Greek letter π in the 1700s. Introduced by William Jones in 1706, use of the symbol was popularized by Leonhard Euler, who adopted it in 1737.
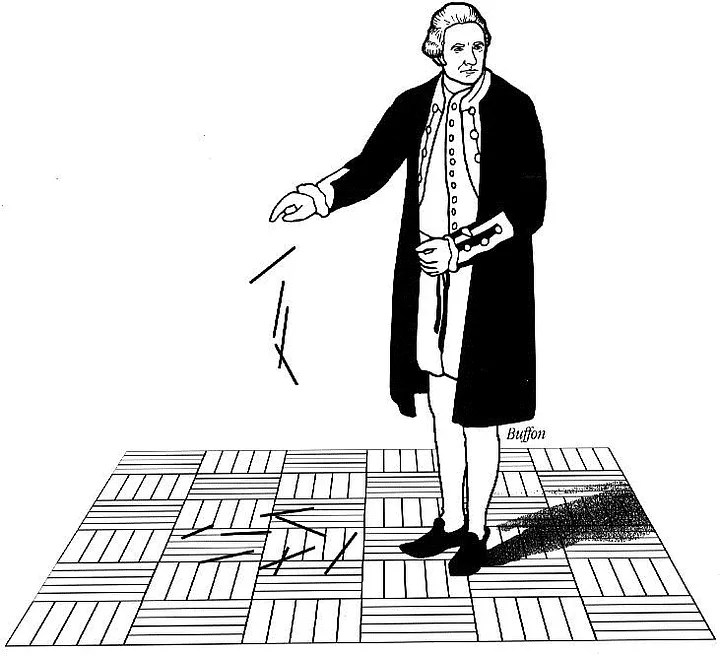
An eighteenth-century French mathematician named Georges Buffon devised a way to calculate π based on probability. [2]
Buffon’s Needle
This estimation of pi is based on a geometrical probability theory developed in the 18th century by French philosopher Georges-Louis Leclerc, Comte de Buffon. He determined that you can estimate the value of pi by dropping straight objects (e.g., toothpicks, craft sticks, or pencils) on a grid of parallel lines separated by a distance equal to the length of the objects thrown. The proportion of sticks crossing a line is directly related to the value of pi, as follows:
Where
- l is the length of the object being dropped
- t is the number of objects tossed
- d is the distance between the lines
- c is the number of objects crossing the line
The more tosses that are recorded, the more accurate the estimation of pi should become.
A needle of length 1 is randomly dropped on a floor with horizontal lines 2 units apart. What is the probability the needle intersects one of the horizontal lines? The answer might surprise you–it involves the constant π!
Everything is hidden in π
Pi shows up in unexpected places in the natural world. The structure of spirals in seashells and galaxies, the shapes of rivers, and the frequencies of musical notes all have connections to pi. Even the shapes of atoms and molecular structures reflect pi-related principles. Scientists use pi in physics, engineering, and even medicine, particularly in fields that involve rotation, oscillation, and waves.
In cosmology, pi appears in calculations related to Einstein’s theory of relativity and the shape of the universe. It’s used to describe the motion of planets and the structure of black holes. Pi also emerges in wave equations, helping to model everything from sound waves to the tides of the ocean. Its appearance across these seemingly unconnected areas underscores the fundamental role of mathematics in explaining the natural world.
Pi is more than a number—it’s a window into infinity, a fundamental aspect of geometry, and a touchstone in human understanding of the universe. As we continue to uncover its mysteries, pi reminds us of the vast, interconnected nature of mathematics and the beauty hidden within numbers. Beyond its humble start in the study of circles, pi remains an endless source of intrigue and inspiration for mathematicians, scientists, and enthusiasts alike. The next time you see “3.14,” remember that it represents much more than a ratio; it’s a doorway into the unknown.
See also: May I have a large container of coffee (π)
References
[1] Craine, Kelly. “The Magic and Mystery of π (Pi).” 2024. Media and Public Relations | Baylor University. March 12. https://news.web.baylor.edu/news/story/2024/magic-and-mystery-p-pi.
[2] “A Brief History of Pi (π)”. 2024. The Exploratorium. Accessed November 9. https://www.exploratorium.edu/pi/history-of-pi.
Additional Reading
“25 Surprising Facts About Pi.” 2024. Pi Day. Accessed November 9. https://www.piday.org/pi-facts/.
“A Short Story about a Magic Number and Sticks on a Table.” 2024. Throwing Sticks. Accessed November 9. https://nils-n.github.io/throwing-sticks/.
“A Slice of Pi (π) Day History.” 2024. The Exploratorium. Accessed November 9. https://www.exploratorium.edu/pi-day/pi-day-history.
Ali. 2024. “A Very Interesting Math Experiment: Discovering Pi by Throwing a Needle.” Medium. Medium. October 16. https://ali.medium.com/a-very-interesting-math-experiment-discovering-pi-by-throwing-a-needle-1fadf89530cd.
Mathematics is like a vast and beautiful garden with wonders waiting to be discovered. Among these wonders, one of the most captivating is the number π, a symbol as intriguing as a rare flower. Since the days of the wise Archimedes, mathematicians have been fascinated by π, exploring its mysteries just as one might admire a garden’s most exquisite bloom.
⭐ Alyze Sam, “Ethereal, Romantic, Mysterious & Completely Memorizing; The REAL Life of Pi.” 2020. Medium. GIVE Nation. March 14. https://medium.com/thegivenation/ethereal-romantic-mysterious-completely-memorizing-the-real-life-of-pi-91205b793457.
Mallik, Sahinur. 2024. “The Enigma of π: An Infinite Odyssey into Mathematics.” Medium. Vivid Depths. November 13. https://medium.com/vivid-depths/the-enigma-of-%CF%80-an-infinite-odyssey-into-mathematics-182cd1ad4bae.
Among the very few mathematical constants, none has seriously bewitched thinking as soundly as π, the so-called ratio of a circle’s circumference to its diameter. π pops up in equations right across the disciplines—in geometry and calculus, physics and engineering, and many more places. Yet, with such simple origins, π remains beyond all end infinitely complex. It is an irrational number that bears infinite, non-repeating digits. This article explores the secrets of π tracing back the historical origins of the mathematical number, portraying its properties, and talking about why it continues to interest mathematicians to date.
“Buffon’s Needle, MSTE, University of Illinois.” 2024. MSTE, University of Illinois. Accessed November 9. https://mste.illinois.edu/activity/buffon/.
Buffon’s Needle is one of the oldest problems in the field of geometrical probability. It was first stated in 1777. It involves dropping a needle on a lined sheet of paper and determining the probability of the needle crossing one of the lines on the page. The remarkable result is that the probability is directly related to the value of pi. This page will present an analytical solution to the problem along with a JavaScript applet for simulating the needle drop in the simplest case scenario in which the length of the needle is the same as the distance between the lines.
“One Million Digits of Pi On One Page!- [Plus Guides And Information].” 2024. Pi Day. Accessed November 9. https://www.piday.org/million/.
“Pickup Sticks & Pi.” 2020. Atom. August 12. https://prancer.physics.louisville.edu/modules/pi/index.html.
We all learn at school that π is the ratio of a circle’s circumference to its diameter, but π turns up all over the place in mathematics. For example, did you know you can measure π just by dropping sticks on a table and counting them? This is because π has a role in statistics too. Below you can try it for yourself, first we’ll visit the story of how this remarkable trick was discovered.
“Pi Toss.” 2024. The Exploratorium. Accessed November 9. https://www.exploratorium.edu/snacks/pi-toss.
Tu, Chau. 2017. “Estimate Pi by Dropping Sticks.” Science Friday. March 14. https://www.sciencefriday.com/articles/estimate-pi-by-dropping-sticks/.
The simulator is based on an experiment called Buffon’s needle, one of the oldest problems in the field of geometrical probability, according to The Mathematica Journal. In the 18th century, French philosopher Georges-Louis Leclerc, Comte de Buffon determined that you can approximate pi by dropping needles on a grid of parallel lines (whose spacing is greater than the length of a needle) and calculating the probability that they will cross a line. The probability is directly related to pi.
Medium Member Only
⭐ I suggest that you read the entire reference. Other references can be read in their entirety but I leave that up to you.
The featured image on this page is from the srkrbcrsvlcuh.blogspot.com website.
Mathematical Mysteries 