Although Pascal was the first mathematician to organize the pattern of binomial coefficients and find multiple uses for it, many others studied the pattern before him. It was discovered by Chinese mathematician Jia Xian, when he discovered a triangle that was a representation of the coefficients in a binomial expansion. This triangle was further popularized by Chinese mathematician Yang Hui, which is why it is often known as the Yanghui triangle in China. Though named after Blaise Pascal (1653), the triangle was known long before—in India as Meru-prastaara (मेरुप्रस्तार), in China as Yang Hui’s triangle (杨辉三角形), in Iran as Khayyám triangle (مثلث خیام), and in Italy as Triangolo di Tartaglia (Tartaglia’s Triangle), named after Niccolò Fontana Tartaglia, a well-known algebraist. The triangle was first published in 1665 in Pascal’s ‘Treatise on Arithmetical Triangle,’ and it was officially called Pascal’s in 1708. [2][8][9]
Definition
For anyone who has experience with mathematics, Pascal’s Triangle should need no introduction. Pascal’s Triangle has been studied for centuries—and for good reason. This simple-looking triangle hides a world of fascinating patterns, from triangular numbers to the famous Fibonacci sequence. It’s a key tool in algebra and a powerful ally in probability and combinatorics. [9]
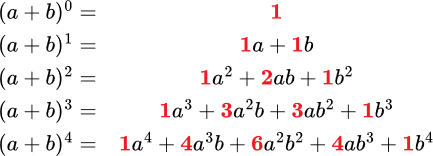
Who
In the real world, Pascal’s Triangle translates into the complex topic of graph theory who’ve includes turning mapping information into data, finding shortest paths, airplane rules and airport control, computer graphics, engineering, data management, search algorithms and more. Pascal’s Triangle is also often used in architecture and design, because since buildings are 3-D, using Pascal’s Triangle in expansions and measurements is common. [3]
What are some real world examples of the use of the binomial theorem? [4]
- Binomial theorem is heavily used in probability theory, and a very large part of the US economy depends on probabilistic analyses. It is most useful in our economy to find the chances of profit and loss which is a great deal with developing economy.
- Binomial theorem and distribution is used in higher mathematics and calculation. Suppose you have given an equation with have degree 28 i.e like 2*x^28 +3*x^27+……..+3. You can find here all 28 roots of x In certain scientific research binomial is very helpful to solve impossible equations.if you have seen Einstein equations there is a lot use of binomial theorem. That is why we have now very great theories and laws by Sir Albert Einstein.
- Moreover binomial theorem is used in forecast services .the future weather forecasting is impossible without binomial theorem.the disaster forecast is also depend upon binomial theorems.
- The selection is the most using application in our life. Popularly known it uses this theorem to give ranks to the candidates.The probability will be impossible without binomial distribution.
- It is used in architecture in giving shape and determining the areas of infrastructure to find about the amount of material to be use in that. it help in the estimation and to find the total expenditure to build the building .so all financial sites depend indirectly on binomial theorem.
What
Many of you already know about Pascal’s triangle. Pascal’s triangle is a triangular arrangement of number that’s really useful in the expansion of any binomial expression, such as (x+y)^n. Not only in algebra, Pascal’s triangle also used in set theory, probability theory and combinatorics. [5]
How do I solve (√a+√b) ^8 with pascal’s triangle? [6]
(We don’t “solve” these, we “expand” them.)
I feel that there is no need to use the old traditional “formula method” or Pascal’s triangle for finding binomial expansions. I much prefer the following approach.
Let’s experiment by looking at a few expansions.
Then, just looking at the NUMBERS (coefficients), we get Pascal’s Triangle:
Many years ago, I read that our old friend, Newton, saw a simple pattern for producing these coefficients without having to use Pascal’s triangle as follows:
This is the simple pattern I would use!
I call this the “thinking method” as opposed to the “formula method”.
I think it would be very instructive and helpful to examine how I have expanded the following without resorting to using some standard general term formula.
How can you memorize Pascal’s Triangle? [7]
It is not a good idea to memorise Pascal’s Triangle!
Suppose you need a few terms of something like…
It is a much better idea to remember a pattern which will work for any sized number.
The pattern is much easier to remember than the general term or Pascal’s triangle!
Now just see how easy it is to expand a few terms of…
Why
- Patterns in the triangle—like doubling, symmetry, and diagonal sequences—help learners see relationships between numbers rather than memorizing isolated facts. This nurtures the kind of mathematical intuition that makes later topics feel natural.
- Each number is the sum of the two above it
- Diagonals reveal counting numbers, triangular numbers, and Fibonacci numbers
- Patterns repeat and grow predictably
- Pascal’s Triangle is a crossroads where multiple branches of math meet. A single diagram becomes a unifying map of mathematical ideas.
- Combinatorics (binomial coefficients)
- Algebra (expanding (a + b)n
- Probability (counting outcomes) [#]
- Geometry (triangular numbers and tetrahedral numbers)
- Number theory (prime patterns, modular arithmetic)
- Strengthens reasoning and creativity. It’s a perfect playground for developing mathematical habits of mind.
- Conjecture (“What happens if…?”)
- Pattern recognition
- Generalization
- Proof and explanation
- Explains real‑world ideas. It’s not just a curiosity—it’s a practical tool.
- Lottery odds
- Genetics probability
- Risk modeling (see Case Study: Triangle of Trades – Pascal’s Path to Risk Diversification)
- Polynomial modeling in science and engineering
See Theoretical Knowledge Vs Practical Application.
How
Combinatorial Numbers
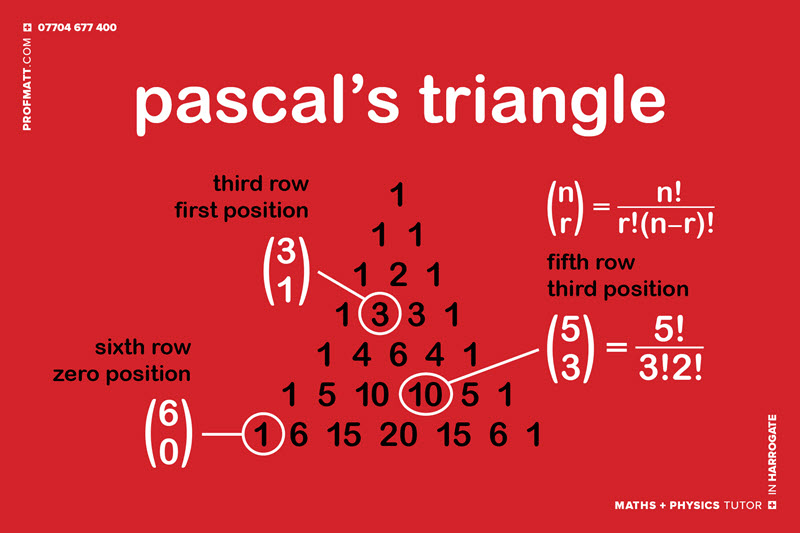
Perhaps the most interesting relationship found in Pascal’s Triangle is how we can use it to find the combinatorial numbers (see featured image above). Recall the combinatorics formula n choose k (if you’re blanking on what I’m talking about check out this post for a review). We find that in each row of Pascal’s Triangle n is the row number and k is the entry in that row, when counting from zero. [1]
Example
How many ways can I choose 2 people out of 6 candidates for a committee?
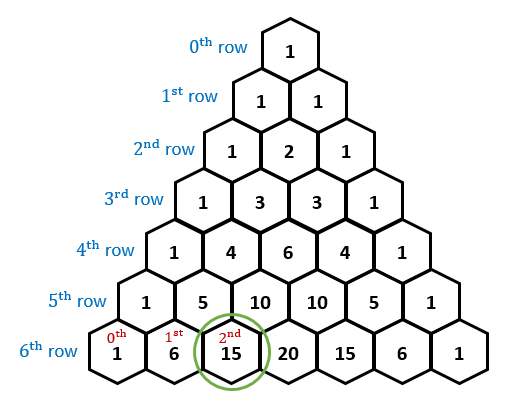
The 2nd number in row 6 = C(6,2) = 15, or
Pascal’s Triangle and Fibonacci Numbers
The process for calculating Fibonacci numbers is to sum the shallow diagonals (also called rising/anti-diagonals or lesser diagonals) of Pascal’s triangle. We sum along the shallow diagonals going down-right (or up-right depending on perspective), usually starting from the left side.
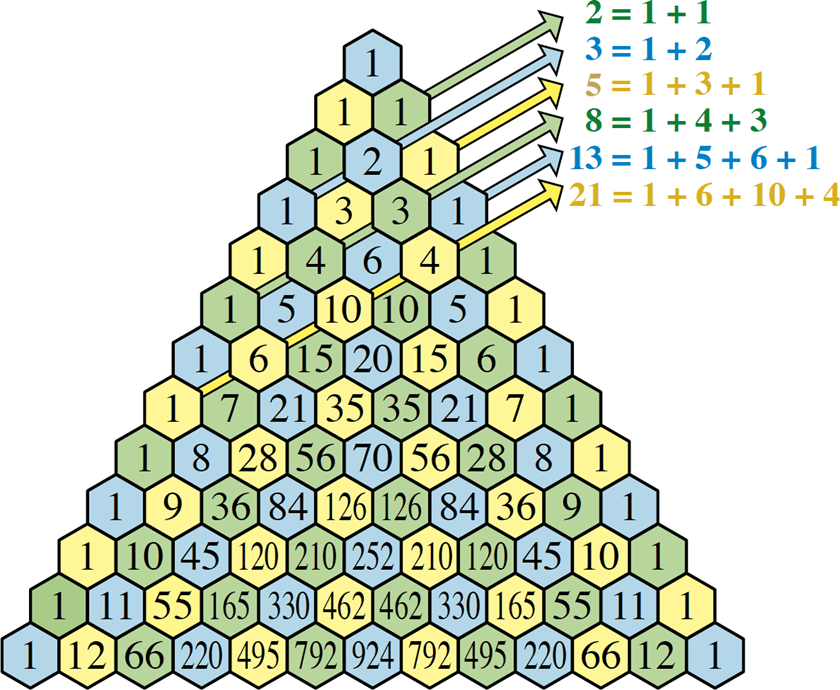
a Fibonacci number. – Archimedes Lab Project
Here are the first few important diagonals in tabular form:
| Diagonal # (k) | Direction | Terms you sum | Fibonacci number |
|---|---|---|---|
| 0 | very first 1 | 1 (row 0) | F₁ = 1 |
| 1 | next diagonal | 1 | F₂ = 1 |
| 2 | 1 + 1 | F₃ = 2 | |
| 3 | 1 + 2 | F₄ = 3 | |
| 4 | 1 + 2 + 1 | F₅ = 5 | |
| 5 | 1 + 3 + 3 + 1 | F₆ = 8 | |
| 6 | 1 + 6 + 5 + 1 | F₇ = 13 | |
| 7 | 1 + 6 + 10 +4 | F₈ = 21 |
The Fibonacci recurrence Fₙ = Fₙ₋₁ + Fₙ₋₂ mirrors the way Pascal’s triangle is built (each entry = sum of two numbers above it). When you move to the next shallow diagonal, you’re effectively picking up contributions from the previous two diagonals — just shifted — which creates the same recurrence pattern as Fibonacci numbers.
Other Aspects of Pascal’s Triangle
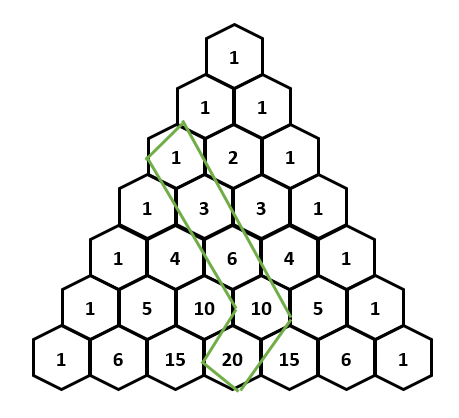
Hockey Stick
Hockey Stick: Start at any of the “1″ elements on the left or right side of Pascal’s triangle. Sum elements diagonally in a straight line, and stop at any time. Then, the next element down diagonally in the opposite direction will equal that sum. This innocent-looking pattern is actually a very powerful summation tool — it’s behind many clever solutions in combinatorics and competitive programming.
If you start at the rth row and end on the nth row, this sum is
Sierpiński Triangle
Sierpiński Triangle: The Sierpiński triangle, also called the Sierpiński gasket or Sierpiński sieve, is a fractal with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles. Originally constructed as a Sierpiński curve, this is one of the basic examples of self-similar sets—that is, it is a mathematically generated pattern reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński but appeared as a decorative pattern many centuries before the work of Sierpiński.
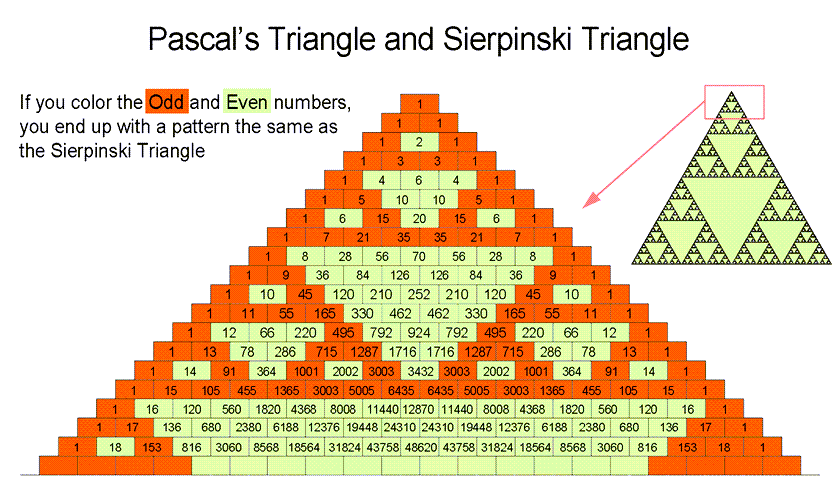
Pascal’s triangle and the Sierpiński triangle are deeply connected: when you take Pascal’s triangle and color its numbers based on whether they are odd or even (often black for odd, white for even), the pattern that emerges is the Sierpiński triangle, a self-similar fractal. The Sierpiński triangle is a geometric shape formed by repeatedly removing the middle triangle from a larger one, and this iterative process mirrors the parity (odd/even) pattern found in the infinite rows of Pascal’s triangle.
Famous Number Sequences
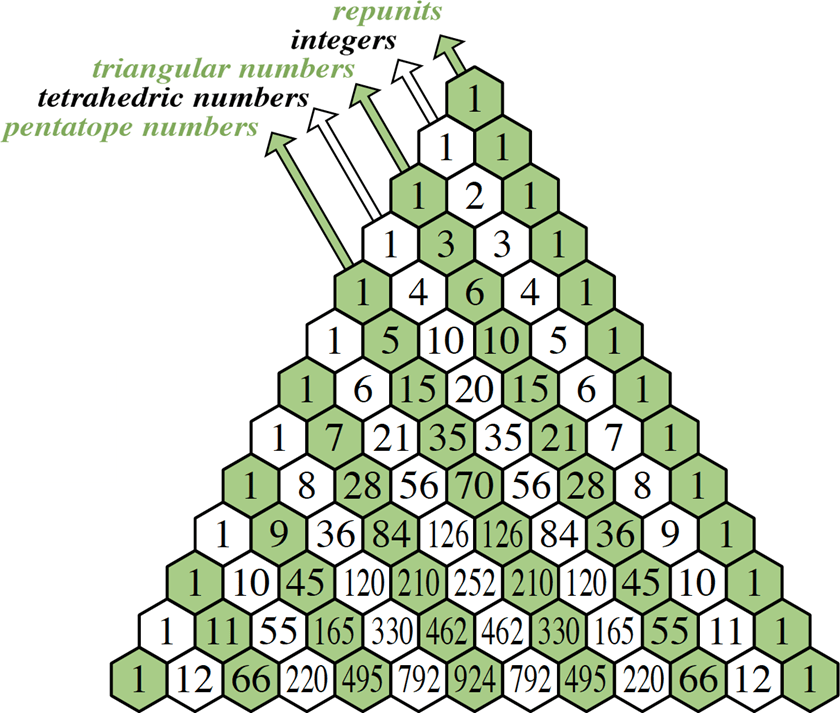
Each diagonal of Pascal’s Triangle, from right to left, contains famous number sequences—repunits, natural numbers, triangular, tetrahedral, pentatope numbers, and higher-dimensional figurate numbers.
- repunit/repdigit – In recreational mathematics, a repunit is a number like 11, 111, or 1111 that contains only the digit 1 — a more specific type of repdigit. The term stands for “repeated unit” and was coined in 1966 by Albert H. Beiler in his book Recreations in the Theory of Numbers.
- natural numbers – In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. The terms positive integers, non-negative integers, whole numbers, and counting numbers are also used. The set of the natural numbers is commonly denoted by a bold N or a blackboard bold ℕ.
- triangular numbers – A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The nth triangular number is the number of dots in the triangular arrangement with n dots on each side, and is equal to the sum of the n natural numbers from 1 to n.
- tetrahedral numbers – A tetrahedral number, or triangular pyramidal number, is a figurate number that represents a pyramid with a triangular base and three sides, called a tetrahedron.
- pentatope numbers – In number theory, a pentatope number (or hypertetrahedral number or triangulo-triangular number) is a number in the fifth cell of any row of Pascal’s triangle starting with the 5-term row 1 4 6 4 1, either from left to right or from right to left. It is named because it represents the number of 3-dimensional unit spheres which can be packed into a pentatope (a 4-dimensional tetrahedron) of increasing side lengths.
- higher-dimensional figurate numbers – The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes (polygonal numbers) and different dimensions (polyhedral numbers). The ancient Greek mathematicians already considered triangular numbers, polygonal numbers, tetrahedral numbers, and pyramidal numbers, and subsequent mathematicians have included other classes of these numbers including numbers defined from other types of polyhedra and from their analogs in other dimensions.
Many of the References and Additional Reading websites and Videos will assist you with understanding and applying Pascal’s Triangle.
As some professors say: “It is intuitively obvious to even the most casual observer.”
References
[1] Berry, Brett. “Top 10 Secrets of Pascal’s Triangle”. 2018. Medium. https://medium.com/i-math/top-10-secrets-of-pascals-triangle-6012ba9c5e23.
[2] Rout, Siddharth. “Pascal’s Triangle”. 2020. Future Bound. https://sidr.hashnode.dev/pascals-triangle.
[3] user371838, “Pascal’s Triangle’s different usages”. 2017. https://math.stackexchange.com/q/2152960.
[4] Yadav, Pradeep. “What are some real world examples of the use of the binomial theorem?” 2023. Quora. https://qr.ae/pyTVtk.
[5] Siahaan, Ivander Jeremy. “What’s The Use of Pascal’s Triangle?” 2023. Medium. https://medium.com/@ivandessiahaan14/whats-the-use-of-pascal-s-triangle-4532c3687527.
[6] Lloyd, Philip. “How do I solve (√a+√b) ^8 with pascal’s triangle?” 2023. Quora. https://qr.ae/pyTJEh.
[7] Lloyd, Philip. “How can you memorize Pascal’s Triangle?” 2023. Quora. https://qr.ae/pypNQV.
[8] Liu, Ewen. “Pascal’s Triangle.” prezi.com, December 18, 2012. https://prezi.com/ns63yt572bto/pascals-triangle/.
[9] “The Many Faces of a Timeless Triangle – Archimedes Lab Project.” Accessed January 18, 2026. https://archimedes-lab.org/2025/07/16/the-many-faces-of-a-timeless-triangle/.
Additional Reading
Anna. “Pascal’s Triangle.” Medium, January 5, 2024. https://anna-1900.medium.com/pascals-triangle-820da6ef43af.
Bansal, Vikas. “The Mathematical Secrets of Pascal’s Triangle.” Boosters, December 12, 2018. https://medium.com/boosters/the-mathematical-secrets-of-pascals-triangle-5f5e29c57533.
Well, that’s just the brief introduction and some brief magical patterns you may see in Pascal’s triangle. You can also see many patterns also like that of Fractals, Sierpiński triangle, etc. But that’s not the end my friend, it is hiding a lot of secrets within and who knows, maybe you may find one someday. And if you could, let me know. I am a big fan of MATHEMATICS. And you know what MATHS is fun.
Davis, Tom. “Exploring Pascal’s Triangle.” geometer.org. November 27, 2006. http://www.geometer.org/matheircles.
This article provides material to help a teacher lead a class in an adventure of mathematical discovery using Pascal’s triangle and various related ideas as the there is plenty of mathematical content here, so it can certainly be used by anyone who wants to explore the subject, but pedagogical advice is mixed in with the mathematics.
[#] Brennan, Declan. “Probability, Relativity and Pascal’s Triangle.” Cantor’s Paradise, June 15, 2020. https://www.cantorsparadise.com/probability-relativity-and-pascals-triangle-d0850a4aff93.
Adding probabilities and velocities have at least two things in common — a maximum and Pascal’s triangle.
Brothers, Harlan. “Pascal’s Triangle: A Secret Unveiled.” Science Spectrum, November 17, 2025. https://sciencespectrumu.com/pascals-triangle-a-secret-unveiled-8844654b94bc.
While Pascal was primarily concerned with its links to probability theory, the triangle also has many wonderful connections to combinatorics, Euclidean geometry, fractal geometry (in the form of the Sierpiński gasket), and numerous number sequences including the Fibonacci series. As I discovered late one night, beyond these many interesting properties, there is one remarkable aspect that had remained hidden — the base of the natural logarithm, e.
Lazarus. “The Math Behind Galton Board and Pascal’s Triangle”. 2022. Medium. https://medium.com/@ozlazarus/the-math-behind-galton-board-and-pascals-triangle-c6f1eca8218b.
The Galton board was invented in 1876 by the Victorian genius Sir Francis Galton and presented an elegant demonstration of how a normal distribution arises from the combination of a large number of random events. It gave Galton key insights into the distribution of human characteristics during his studies on heredity. It also played a pivotal role in his development of statistical theory, concepts that remain fundamental today.
Mahato, Prabhat. “The Peculiarity of Pascal’s Triangle.” Intuition, April 21, 2023. https://medium.com/intuition/the-peculiarity-of-pascals-triangle-abaabd55a198.
Pascal’s Triangle is one of the most important treasure troves for all the mathematicians since centuries. But what’s so special about it? Isn’t it just a stack of numbers formed by the addition arranged in triangular pattern? Well no! It is much more than just addition. Let’s fully understand Pascal’s triangle.
Motazedi, Tina. “The Pascal Triangle.” Math 341. 10 June 2008. https://math.bu.edu/people/kost/teaching/MA341/Tina.pdf.
Blaise Pascal was born at Clermont-Ferrand, in the Auvergne region of France on June 19, 1623. In 1653 he wrote the Treatise on the Arithmetical Triangle which today is known as the Pascal Triangle. Although other mathematicians in Persia and China had independently discovered the triangle in the eleventh century, most Of the properties and applications of the triangle were discovered by Pascal. This triangle was among many of Pascal’s contributions to mathematics. He also came up with significant theorems in geometry, discovered the foundations of probability and calculus and also invented the Pascaline calculator but he is best known for his contributions to the Pascal triangle.
 Müller, Kasper. “Mysterious Patterns in Pascal’s Triangle.” Cantor’s Paradise, May 29, 2023. https://www.cantorsparadise.com/mysterious-patterns-in-pascals-triangle-b8bad8d494e3.
Müller, Kasper. “Mysterious Patterns in Pascal’s Triangle.” Cantor’s Paradise, May 29, 2023. https://www.cantorsparadise.com/mysterious-patterns-in-pascals-triangle-b8bad8d494e3.
There are many many more patterns to explore than these and in fact, to this day, people are finding new ones. This mathematical beauty just keeps on giving.
Pallavi. “Pascal’s Triangle.” Helping with Math, January 1, 2022. https://helpingwithmath.com/pascals-triangle/.
Mathematics is a world of numbers. We have different sets of numbers that can be arranged in different sequences and patterns. One such arrangement of numbers is the Pascal’s triangle. What is it and who invented it?
“Pascal’s Triangle.” BYJU’S, July 30, 2017. https://byjus.com/maths/pascals-triangle/.
Pascal’s Triangle is a kind of number pattern. Pascal’s Triangle is the triangular arrangement of numbers that gives the coefficients in the expansion of any binomial expression. The numbers are so arranged that they reflect as a triangle. Firstly, 1 is placed at the top, and then we start putting the numbers in a triangular pattern. The numbers which we get in each step are the addition of the above two numbers. It is similar to the concept of triangular numbers. In this article, we are going to learn Pascal’s triangle history, definition, properties, patterns, formulas and examples with a complete explanation.
⭐ “Pascal’s Triangle.” CK-12 Foundation, January 14, 2026. https://www.ck12.org/probability/pascals-triangle-binomial-expansion/lesson/pascals-triangle/.
“Pascal’s Triangle.” Brilliant. Accessed January 17, 2026. https://brilliant.org/wiki/pascals-triangle/.
Sid. “8 Secrets of Pascal’s Triangle.” Cantor’s Paradise, January 8, 2023. https://www.cantorsparadise.com/8-secrets-of-pascals-triangle-349cb5e46b09.
Pascal’s triangle may seem like just a triangle of numbers, but it has many secrets that lie just underneath the surface. There are many other characteristics, ranging from the fields of trigonometry to the Golden Ratio.
⭐ Socaci, Adina. “Pascal’s Triangle: The Enigmatic Elegance of Mathematical Patterns.” Medium, September 11, 2023. https://adinasocaci.medium.com/pascals-triangle-the-enigmatic-elegance-of-mathematical-patterns-b66d5d85fe3a.
As we wrap up this mathematical exploration, it’s essential to recognize that, similar to Pascal’s Triangle, the domain of mathematics presents itself as a complex and interconnected structure, poised for investigation. With each discovery, it unveils novel insights and phenomena, reflecting the depth and intricacy of mathematical study.
“Treatise on Arithmetical Triangle.” Accessed January 18, 2026. https://www.cut-the-knot.org/arithmetic/combinatorics/PascalTriangle.shtml.
Videos
Pascal’s triangle, which at first may just look like a neatly arranged stack of numbers, is actually a mathematical treasure trove. But what about it has so intrigued mathematicians the world over? Wajdi Mohamed Ratemi shows how Pascal’s triangle is full of patterns and secrets.
Think you know everything about Pascal’s Triangle? Watch this video and be surprised. You’ll even see how Pi and e are connected!
Brett explains the difference between combinations and permutations and demonstrates how to solve a classic card counting problem both through reasoning and by applying the choose and permutate formulas. In today’s episode, you will learn when to use the combinations, or choose, formula and when to use the permutations formula as well as gain a deep understanding behind the formulas and combinatorics. You will also be introduced to factorial notation. We begin the lesson by solving, through reasoning, how many different 5-card hands can be drawn from a standard deck of 52 cards using slot diagrams. In the process we will uncover both formulas for permutations and combinations.
We illustrate here what Sierpiński Triangles are as fractals, and look at how Pascal’s Triangles can form the Sierpiński Triangles.
 Medium Member Only
Medium Member Only
⭐ I suggest that you read the entire reference. Other references can be read in their entirety but I leave that up to you.
The featured image on this page is from the MATHS + PHYSICS TUTOR IN HARROGATE AND ONLINE website.