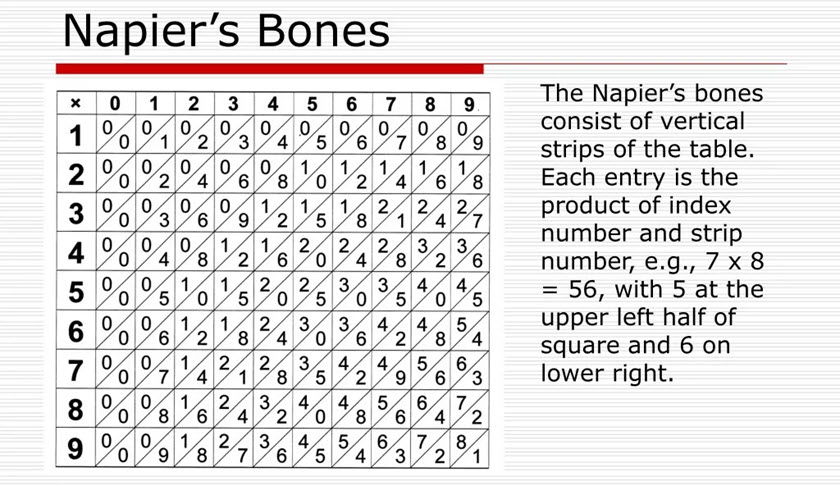
Napier’s bones are a manual calculating device invented by Scottish mathematician John Napier in 1617 to simplify multiplication, division, and square roots by converting them into addition and subtraction, using numbered rods (often made of wood or ivory) with multiplication tables. Users align rods for the digits of the numbers, then read results by adding numbers in specific rows diagonally, a method based on lattice multiplication that is also called rabdology. [1]
- Napier’s bones were widely used for centuries as an early form of calculator.
- The principles of lattice multiplication used in Napier’s bones influenced later tools, including the slide rule. [3]
The origin of Napier’s rods are somewhat of a historical puzzle. He is generally given the entire credit for their invention, yet there are indications of their earlier use. First described in Rabdology, published after his death, they were already well known and available from a number of craftsmen and instrument makers. In his Rabdology dedication, he states: “I had two reasons for making my book about the manufacture and use of the rods available to the public. The first was that the rods have found favor with so many people that they could almost be said to be already in common use both at home and abroad. The other was that it was brought to my attention…that you had kindly advised me to publish them lest they be published under someone else’s name…” [3]
Example Use
There are ten bones corresponding to the digits 0-9, and a special eleventh bone that is used the represent the multiplier. The multiplier bone is simply a list of the digits 1-9 arranged vertically downward. The remainder of the bones each have a digit written in the top square, with the multiplication table for that digits written downward, with the digits split by a diagonal line going from the lower left to the upper right. In practice, multiple sets of bones were needed for multiplication of numbers containing repeated digits.

To multiply two numbers, arrange the bones as described above. The illustration on the right shows this process for 7 x 4896. The computation proceeds from right to left, starting with the rightmost bone in the row determined by the multiplier. In this case, the last digit in the 7s row of the 6-bone is 2, so write down 2. Now add the two adjacent numbers in the same row to the left (i.e., the ones in the parallelogram) to obtain 3 + 4 = 7, which is the next digit, so we now have 72. The next sum is 6 + 6 = 12, so write down the 2 two obtain 272 and carry the 1. Proceeding to the next digit, it is 8 + 5 + = 14 (because of the carry), so write down the 4 to obtain 4272 and carry the 1. The leftmost digit is then 2 + 1 = 3 (from the carry), giving the final answer 7 x 4896 = 34,272. [2]
How Napier’s Bones Can Be Used in Teaching
Napier’s Bones are more than a historical curiosity—they’re a brilliant hands-on tool for helping students *see* multiplication, understand place value, and build confidence with multi‑digit operations. Modern teaching resources emphasize exactly this: they simplify large calculations and make the structure of multiplication visible. Below is a breakdown of how they support learning and how you can use them effectively in the classroom. [4][5][6]
Strengthen Place-Value Understanding
Napier’s Bones break numbers into their digits and show how each digit contributes to the final product. Students can see:
- Each rod represents a digit 0–9.
- Each row shows multiples of that digit.
- Diagonals separate tens and ones.
This visual decomposition helps students understand why, for example, 34 x 7 is really (30 x 7) + (4 x 7).
Make Multi-Digit Multiplication Concrete
- Instead of jumping straight to the standard algorithm, students manipulate rods and read off partial products. This supports:
- Conceptual understanding before procedural fluency
- Reduced cognitive load
- A bridge between arrays, area models, and algorithms
Hands-On Construction Builds Ownership
MathBait encourages students to *build their own set* of bones using popsicle sticks or printables, which turns the tool into a creative project. This supports:
- Fine motor skills
- Spatial reasoning
- A sense of mathematical craftsmanship
- Deeper engagement (students love using tools they made themselves)
Scaffolded Practice and Differentiation
Teachers can use Napier’s Bones to:
- Provide structured practice for students who struggle with multiplication
- Offer an extension activity for students exploring historical calculation tools
- Support learners who benefit from visual or kinesthetic approaches
- Introduce alternative algorithms to build flexible thinking
Build Mental Math and Estimation Skills
Because students must read diagonals and combine partial products, they naturally begin estimating:
- “Does this answer make sense?”
- “Which diagonal contributes the tens?”
- “What happens if I shift this rod?”
This reinforces number sense—something you already emphasize in your mental math materials.
Connect Math to History and Innovation
Napier’s Bones open the door to:
- The history of computation
- John Napier’s role in logarithms
- Pre‑calculator engineering and navigation
- How tools shape mathematical thinking
This makes math feel human, inventive, and alive—perfect for middle schoolers who love stories.
Why Napier’s Bones Are So Effective
They combine:
- Visual structure
- Hands-on manipulation
- Historical context
- Conceptual clarity
- Student agency
References
[1] “Mathematical Instrument Invented by John Napier.” 2003. wikipedia.org. Wikimedia Foundation, Inc. June 24, 2003. https://en.wikipedia.org/wiki/Napier%27s_bones.
[2] “Napier’s Bones.” 2025. Wolfram.com. Wolfram Research, Inc. 2025. https://mathworld.wolfram.com/NapiersBones.html.
[3] “John Napier’s Bones.” 2025. 17centurymaths.com. 2025. https://www.17centurymaths.com/contents/napier/jimsnewstuff/Napiers%20Bones/NapiersBones.html.
[4] “Create Your Own Bones! | MathBait.” 2021. MathBait. 2021. https://www.mathbait.com/multiplication/create-your-own-bones!.
[5] “Multiplication Using Napier’s Bones PowerPoint Lesson KS2-KS3.” 2023. tes.com. 2023. https://www.tes.com/teaching-resource/multiplication-using-napier-s-bones-powerpoint-lesson-ks2-ks3-12935608.
[6] “KS2 Napier Bones Multiplication Maths Activity Sheet.” 2025. twinkl.com. Twinkl. February 12, 2025. https://www.twinkl.com/resource/napier-bones-maths-activity-sheet-t-m-1739379487.
Additional Reading
“1911 Encyclopædia Britannica/Napier, John.” 2017. wikisource.org. Wikimedia Foundation, Inc. February 3, 2017. https://en.wikisource.org/wiki/1911_Encyclop%C3%A6dia_Britannica/Napier,_John.
Bruderer, Herbert. 2021. “How Does One Divide with Napier’s Rods?” acm.org. Communications of the ACM. September 9, 2021. https://cacm.acm.org/blogcacm/how-does-one-divide-with-napiers-rods/.
“Counting Bones | Royal Society.” 2021. royalsociety.org. July 26, 2021. https://royalsociety.org/blog/2021/08/counting-bones/.
Poccia, Danilo. 2023. “Napier’s Bones and the Birth of Logarithms.” Medium. Chronicles of Computation. August 8, 2023. https://medium.com/chronicles-of-computation/napiers-bones-and-the-birth-of-logarithms-8cf60e63f885.
Vaness, Dave.. 2019. “Using Napier’s Bones.” Instructables. November 24, 2019. https://www.instructables.com/Using-Napiers-Bones/.
Videos
FI: Medieval Mathematics: Napier’s Bones, Logarithm & Slide Rule Overview