Matrix Determinants

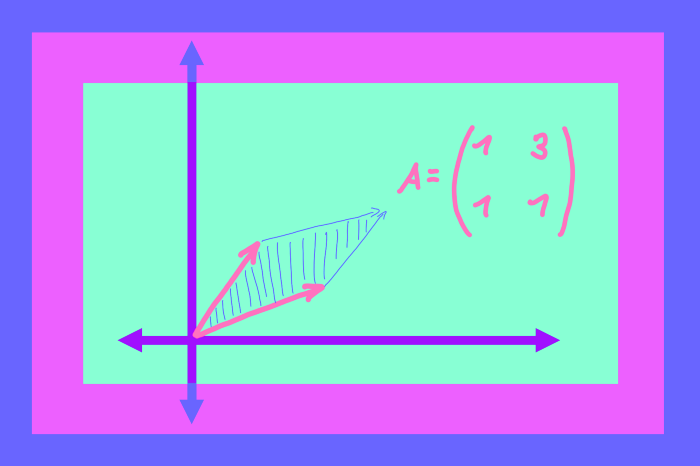
The geometric intuition behind determinants could change how you think about them.

Definition

For a square matrix, i.e., a matrix with the same number of rows and columns, one can capture important information about the matrix in a just single number, called the determinant. The determinant is useful for solving linear equations, capturing how linear transformation change area or volume, and changing variables in integrals. [6]

Who

For those who learned about matrix determinants in a linear algebra course and presentation of the material may have been very dry and mathematical. So you do not understand the usefulness of determinants. You are not alone. Here is what some have said about learning linear algebra:

Despite two linear algebra classes, my knowledge consisted of “Matrices, determinants, eigen something something”. [2]

What

In mathematics, how to compute something should never be the first question. The first question is always: “What really IS it?” Only then should we ask: “Ok now that we know what it is, how can we compute it.”

The determinant of a matrix is the factor by which areas are scaled by this matrix.

However, regarding matrix determinants, I was taught that they are numbers for matrices, how to compute them, and not much more. It took until my university courses that I learned the beauty behind determinants.

As soon as I learned about determinants’ geometric meaning, I was wondering why this wasn’t already taught in high school as it is very easy to understand and mind-opening. [1]

---

The determinant is the “size” of the output transformation. If the input was a unit vector (representing area or volume of 1), the determinant is the size of the transformed area or volume. A determinant of 0 means matrix is “destructive” and cannot be reversed (similar to multiplying by zero: information was lost). [2]

---

Whatever area in the input space we choose, it seems that after the transformation the area gets bigger. This is precisely what the determinant is!

The determinant of a matrix is the factor by which areas are scaled by this matrix.

Because matrices are linear transformations it is enough to know the scaling factor for one single area to know the scaling factor for all areas. [1]

---

Presumably, you think of determinants as operations applied to matrices. So first, let’s examine what matrices “really are”: When you multiply a matrix by the coordinates of a point, it gives you the coordinates of a new point. In this way, we can think of a matrix as a transformation which turns points in space into different points in space. And this is what matrix arithmetic is all about: matrices represent transformations (specifically, so-called “linear” transformations).

The determinant of a transformation is just the factor by which it blows up volume (in the sense appropriate to the number of dimensions; “area” in 2d, “length” in 1d, etc.). If the determinant is 3, then it triples volumes; if the determinant is 1/2, it halves volumes, and so on.

(The one nuance to add to this is that we are actually speaking about “oriented” volume. That is, our transformation may or may not turn figures inside out (e.g., in 2d, it might turn clockwise into counterclockwise; in 3d, it might turn left-hands into right-hands). If it does turn figures inside out, its determinant is considered negative.)

So, for example, in 3d: any rotation has determinant 1 because it leaves volume unchanged. Scaling everything up by a factor of 2 has determinant 2323 because that’s the factor by which it increases volume. Projecting everything onto a plane has determinant 0, because it flattens everything to volume 0. Any reflection has determinant -1, because it turns everything inside out but otherwise leaves volume unchanged. And so on…

Finally, one useful observation: if you take a transformation which multiplies volume by, say, 5, and follow it up with a transformation which multiplies volume by 3, then overall, volume will multiply by 5 * 3. Multiplying matrices amounts to chaining transformations end-to-end in this manner, so the determinant of a product of matrices is the product of their determinants.

[The reason a linear transformation has to blow up all regions’ volumes by the same factor, should you care, is this: You can always think of any region as made up of lots of tiny regions, all identical except for their position. Each of these tiny regions is transformed in the same exact way except for position (this is the “linearity”), so the big region blows up by the same factor as each of the tiny regions. So, you can think of the determinant as the amount by which your favorite tiny shape scales in volume, and rest assured that all other regions scale by the same factor as well.] [9]

Why

See Theoretical Knowledge Vs Practical Application.

How

I don’t show you how to compute determinants. Many of the References, Additional Reading, websites and YouTube videos will assist you with that.

As some professors say: “It is intuitively obvious to even the most casual observer.”

Cramer’s Rule

The Cramer’s rule provides a method of solving a system of linear equations through the use
of determinants. The Hessian [4][5] can be used for a test whether a given critical point is a local
minimum or maximum of a function of two or more real variables. In the article the use of the
Cramer’s rule and the Hessian is demonstrated on economic optimization problems.

Determinants and Cramer’s rule are important tools for solving many problems in business
and economy. Especially for searching an optimal solution of the maximization profit or
minimization cost problems it can be very often apply. [3]

Applying Cramer’s Rule

I try not to provide examples unless I think they are needed. In this case, this example shows the usefulness of matrices and Cramer’s Rule. [7][8]

Cramer’s rule is a way of solving a system of linear equations using determinants. Suppose we are trying to solve a system of linear equations such as the following.

2x – 3y + z = 11
x + 4y – 2z = -3
4x – 5y + 3z = 19

or Ax = b in matrix form, where

 

To find the value of each variable, you divide the determinant of each corresponding modified matrix by the determinant of the coefficient matrix.

 

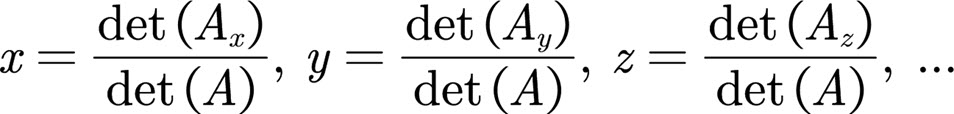
For our example, the determinant of the coefficient matrix A is as follows.

 

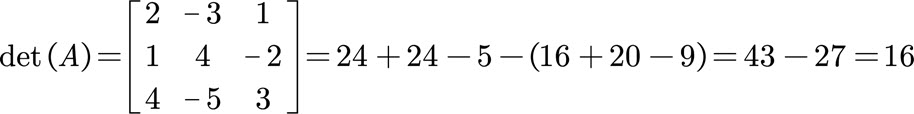
The corresponding modified matrix A_i is a new matrix formed by replacing the ith column of A with the b vector.

 

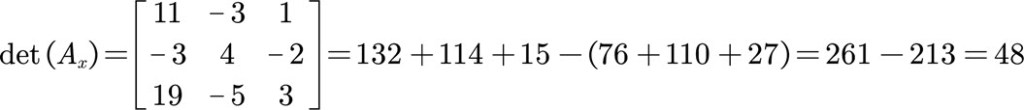
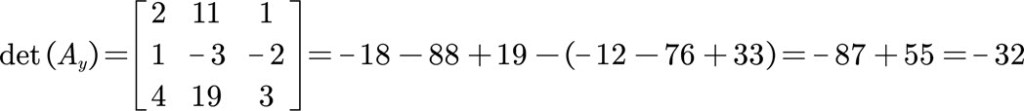
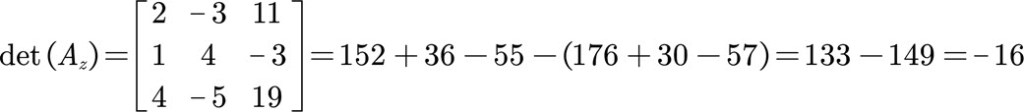
Using Cramer’s rule and doing the dividing.

 

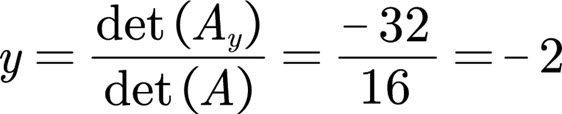
So the solution to the system of equations is x = 3, y = -2, z = -1.

Limitations of Cramer’s rule

• Because we are dividing by det(A) to get , Cramer’s rule only works if det(A) ≠ 0. If det(A) = 0, Cramer’s rule cannot be used because a unique solution does not exist since there would be infinitely many solutions, or no solution at all.
• Cramer’s rule is slow because we have to evaluate a determinant for each x_i. When we evaluate each det(A_i) we have to perform Gaussian elimination on each A_i for a total of n times. In comparison, if we were to use the augmented matrix, [A|b], we would only need to perform Gaussian elimination once to solve Ax = b.

Application

“Applications Of Matrices And Determinants – GeeksforGeeks”. 2021. GeeksforGeeks. https://www.geeksforgeeks.org/applications-of-matrices-and-determinants/.

“6.5 – Applications Of Matrices And Determinants”. 2021. people.richland.edu. https://people.richland.edu/james/lecture/m116/matrices/applications.html.

References

 [1] “What Really IS A Matrix Determinant?” 2021. Medium. https://towardsdatascience.com/what-really-is-a-matrix-determinant-89c09884164c.

[2] “An Intuitive Guide to Linear Algebra”. 2021. betterexplained.com. https://betterexplained.com/articles/linear-algebra-guide/.

[3] Valentová, Eva. DETERMINANTS AND THEIR USE IN ECONOMICS. 2021. opf.slu.cz. http://www.opf.slu.cz/aak/2011/03/valentova.pdf.

[4] “The Hessian Matrix | Multivariable Calculus (Article) | Khan Academy”. 2021. Khan Academy. https://www.khanacademy.org/math/multivariable-calculus/applications-of-multivariable-derivatives/quadratic-approximations/a/the-hessian.

The Hessian is a matrix that organizes all the second partial derivatives of a function.

[5] https://qr.ae/pyZEd3″Hessian Matrix | Brilliant Math & Science Wiki”. 2021. brilliant.org. https://brilliant.org/wiki/hessian-matrix/.

The Hessian Matrix is a square matrix of second ordered partial derivatives of a scalar function. It is of immense use in linear algebra as well as for determining points of local maxima or minima.

[6] “The Determinant Of A Matrix – Math Insight”. 2021. mathinsight.org. https://mathinsight.org/determinant_matrix.

[7] Sterling, Mary Jane. Linear Algebra for Dummies. Hoboken, NJ: Wiley Publishing, Inc., 2009.

[8] “Cramer’s rule”. 2022. Math.net. https://www.math.net/cramers-rule.

[9] Ramesh, Sridhar. “What are intuitive explanations for determinants?”. 2023. Quora. https://qr.ae/pyZEd3.

Additional Reading

“Determinants: Definition”. 2021. textbooks.math.gatech.edu. https://textbooks.math.gatech.edu/ila/determinants-definitions-properties.html.

The determinant is a function

det: {square matrices} → R

satisfying the following properties:

1. Doing a row replacement on A does not change det ( A ) .
2. Scaling a row of A by a scalar c multiplies the determinant by c.
3. Swapping two rows of a matrix multiplies the determinant by −1.
4. The determinant of the identity matrix I_n is equal to 1.

In other words, to every square matrix A we assign a number det ( A ) in a way that satisfies the above properties.

In each of the first three cases, doing a row operation on a matrix scales the determinant by a nonzero number. (Multiplying a row by zero is not a row operation.) Therefore, doing row operations on a square matrix A does not change whether or not the determinant is zero.

The main motivation behind using these particular defining properties is geometric: see Section 4.3. Another motivation for this definition is that it tells us how to compute the determinant: we row reduce and keep track of the changes.

---

“Understanding Properties Of Determinants | College Algebra”. 2021. courses.lumenlearning.com. https://courses.lumenlearning.com/ivytech-collegealgebra/chapter/understanding-properties-of-determinants/.

A General Note: Properties of Determinants

1. If the matrix is in upper triangular form, the determinant equals the product of entries down the main diagonal.
2. When two rows are interchanged, the determinant changes sign.
3. If either two rows or two columns are identical, the determinant equals zero.
4. If a matrix contains either a row of zeros or a column of zeros, the determinant equals zero.
5. The determinant of an inverse matrix A​−1​​ is the reciprocal of the determinant of the matrix A.
6. If any row or column is multiplied by a constant, the determinant is multiplied by the same factor.

---

V, Uma. 2021. “Applications Of Determinants And Matrices: Meaning, Solved Examples”. Embibe Exams. https://www.embibe.com/exams/applications-of-determinants-and-matrices/.

There are many applications of matrices and determinants in daily life and various fields of science, ranging from statistical studies of a population to encrypting data in cryptography to remain confidential. When it comes specifically to mathematics, one of the most important applications is to solve a system of n linear equations in n variables using Cramer’s Rule and to use the Inverse Matrix Method. Though both use determinant operations, the latter is discussed in detail in this article. Before going into the details, let us understand the basics and applicants of matrices and determinants.

“I have been studying matrices for over a year now, no one can prove to me that the determinant of a matrix gives something concrete other than “it just works so accept it and move on”. Can someone here do better or point me to a proof?” 2024. Quora. Accessed August 4. https://qr.ae/p2IThT.

Determinant of a 2×2 matrix gives us the scale factor by which the area of the original shape is increased by. (I didn’t say decrease because in that case, the determinant will be less than 1 so it all works out nicely). In a similar way, the determinant of a 3×3 matrix gives the scale factor for volumes.

Margalit, Dan and Joseph Rabinoff. 2022. “4.3: Determinants and Volumes.” Mathematics LibreTexts. LibreTexts. September 17. https://math.libretexts.org/Bookshelves/Linear_Algebra/Interactive_Linear_Algebra_(Margalit_and_Rabinoff)/04:_Determinants/4.03:_Determinants_and_Volumes.

In this section we give a geometric interpretation of determinants, in terms of volumes. This will shed light on the reason behind three of the four defining properties of the determinant, Definition 4.1.1 in Section 4.1. It is also a crucial ingredient in the change-of-variables formula in multivariable calculus.

Videos

 

 

View the complete Linear Algebra course: http://ocw.mit.edu/18-06S05. This is a basic subject on matrix theory and linear algebra. Emphasis is given to topics that will be useful in other disciplines, including systems of equations, vector spaces, determinants, eigenvalues, similarity, and positive definite matrices.

 

 

My intention was to convey the visual intuitions surrounding the determinant rather than provide rigorous proofs, of which many can be found from many textbooks. As such, I left out more technical aspects of the mathematics involved. In the video, we showed that if there exists a function satisfying the five rules, it must have the form given by the Leibniz formula (uniqueness), but we did not show that the Leibniz formula actually satisfied those five rules (existence). Similarly, I chose to avoid any discussion of defining area and volume via the Lebesgue measure and proving that the determinant does indeed measure volume in this sense — these formalisms detract from the intuitions I am trying to convey. For similar reasons I avoided mentioning the exterior algebra and geometric algebra — every abstraction comes with a pedagogical cost. Also, (-1)^sign is often taken to be the definition of the sign of a permutation, rather than just the sign function I introduced.

---

 Medium Member Only

---

The featured image on this page is by Marcel Moosbrugger.