Nicholas Bourbaki
Nicholas Bourbaki was not a person but a pseudonym chosen for a secretive math group founded by nine great mathematicians in France in the mid-1930s. Henri Cartan, André Weil, Szolem Mandelbrojt, Frenchmen Claude Chevalley, and Jean Dieudonne were some of the active founders who collectively wrote many academic papers under the Bourbaki pseudonym to represent the essence of a “contemporary mathematician.”
⭐ Aczel, Amir D. 2006. The Artist and the Mathematician. The Story of Nicolas Bourbaki, the Genius Mathematician Who Never Existed. New York, NY: Thunder’s Mouth Press.
Nicolas Bourbaki, whose mathematical publications began to appear in the late 1930s and continued to be published through most of the twentieth century, was a direct product as well as a major force behind an important revolution that took place in the early decades of the twentieth century that completely changed Western culture. Pure mathematics, the area of Bourbaki’s work, seems on the surface to be an abstract field of human study with no direct connection with the real world. In reality, however, it is closely intertwined with the general culture that surrounds it. Major developments in mathematics have often followed important trends in popular culture; developments in mathematics have acted as harbingers of change in the surrounding human culture. The seeds of change, the beginnings of the revolution that swept the Western world in the early decades of the twentieth century both in mathematics and in other areas were sown late in the previous century. This is the story both of Bourbaki and the world that created him in that time. It is the story of an elaborate intellectual joke because Bourbaki, one of the foremost mathematicians of his day never existed.
“The Genius Mathematician That Never Lived”. 2021. Medium. https://madiha-7874.medium.com/the-genius-mathematician-that-never-lived-46879f8e13bb.
When observing the recent past of mathematical history, you encounter the name Nicolas Bourbaki quite often. The reason for this is quite simple, actually. Nicolas Bourbaki, born 1935, might be the author of the most math books in history. More importantly, he has written books ranging from mathematical history to algebraic topology, and even calculus. Where it becomes mysterious, however, is that not a single person has seen him. That is because no one by the name of Nicolas Bourbaki has ever lived.
Ali. “The Secret Math Society: Nicolas Bourbaki”. 2022. Medium. https://ali.medium.com/the-secret-math-society-nicolas-bourbaki-59c05f1a67f3.
Marcus du Sautoy argues that mathematics is the driving force behind modern science: mathematical secrets of Nicholas Bourbaki.
Ali. 2024. “The Interesting Story of the Mathematician Who Never Existed: Nicolas Bourbaki.” Medium. Medium. June 30. https://ali.medium.com/the-interesting-story-of-the-mathematician-who-never-existed-nicolas-bourbaki-43ca56b7d8ba.
Bourbaki’s most important rule was that they did not accept any mathematician over the age of fifty into their group. Once a member reaches fifty, their membership would be withdrawn and their authority revoked. They believed that someone aged fifty would have a hard time adapting to the ideas of someone in their twenties or thirties.
Hemanth. “The Story Of The Rockstar Mathematician Who Never Lived”. 2022. Medium. https://medium.com/street-science/the-story-of-the-rockstar-mathematician-who-never-lived-ac523b64a5b4.
The story begins at the prestigious school: École normale supérieure (ENS) in France. In the early 1900s, a student named André Weil had attended the school. During his time there, a new professor had presented a certain “theorem of Bourbaki.” Later on, it turned out that this new professor was just an upperclassman who was pulling a prank. Somehow, the narrative and the humour of this prank stuck with Weil.
Road, Silk. “What has been Nicolas Bourbaki’s influence on modern mathematics? How would it have shaped up without them?”. 2023. Quora. https://qr.ae/pyKyeO.
They are all Nicolas Bourbaki
Nicolas Bourbaki was a genius mathematician who never existed. He was actually a group of French mathematicians who decided to write a series of books on modern mathematics under a fake name. Why? Because they were bored with the old-fashioned textbooks and wanted to create a new, rigorous and abstract vision of their discipline. They also liked to prank their colleagues and have fun with their secret identity.
Bourbaki’s influence on modern mathematics was huge. He introduced new concepts, notations and terminology that are now widely used, such as injective, surjective and bijective functions. He also unified different branches of mathematics, such as algebra, topology and analysis, by using a common axiomatic framework. He showed that mathematics was not just a collection of facts and formulas, but a coherent and logical system that could be explored and developed.
But not everyone was happy with Bourbaki’s style. Some critics accused him of being too abstract, too formal and too elitist. They argued that he ignored the intuition, the history and the applications of mathematics. They also complained that he made mathematics too difficult and inaccessible for students and teachers. Some even suspected that he was part of a communist plot to undermine Western civilization.
It’s hard to say how mathematics would have shaped up without Bourbakire, but maybe it would have been less elegant, less general and less rigorous. Maybe it would have been more diverse, more concrete and more relevant. Maybe it would have been more or less the same. Who knows? One thing is certain: it would have been less mysterious, less amusing and less surprising. Because Bourbaki was not just a mathematician; he was also a legend, a myth and a joke.
Georg Cantor
The mathematician Georg Cantor was born in St. Petersburg, Russia, on March third, 1845. His family moved to Germany when he was 11. As a youth, he excelled in maths and was an outstanding violinist. He went on to study maths at the University of Berlin under some of the great’s of the day, including Leopold Kronecker, Karl Weierstrass. Later, his research led him to consider infinity, not just some abstract concept, but a new type of number, a transfinite number.
What is something that is trivial to a mathematician but would amaze a layperson?
One of the most beautiful mathematical facts that are (currently) trivial to a mathematician, but would amaze a layperson is this:
“Some infinities are bigger than others”.
If anyone tells you that this is obvious, they are lying. Proving this is my favorite lecture when I teach Discrete Math I.
This was proven in the 1870s by Georg Cantor. A number of mathematicians didn’t accept Cantor’s proof, at least for a while.
Cantor essentially showed that the cardinality of the set of Real Numbers is greater than that of the Natural Numbers. He did this by showing that no matter how you tried to pair up the Reals with the Naturals, there would always be some Reals that were not used.
Ever weirder, given any infinite set, we can create a greater infinite set. This leaves us with this beautiful statement:
“Given an infinite set, there is an infinite set with a greater order of infinity.”
Incredible.
In 1900, the great mathematician, David Hilbert (1862 – 1943), gave a widely regarded talk about some of the unsolved problems in mathematics. During this talk he mentioned Cantor’s proof that the set of Reals is a higher order of infinity than the set of Natural Numbers. He then said:
“Nothing will remove us from the paradise that Cantor has created for us.”
Farage, Tim. “What Is Something That Is Trivial To A Mathematician But Would Amaze A Layperson?” 2022. Quora. https://qr.ae/pv5F0m.
“A Lonely Mathematician At The Edge Of Infinity: Georg Cantor”. 2021. Medium. https://mathladyhazel.medium.com/a-lonely-mathematician-at-the-edge-of-infinity-georg-cantor-62d36729761.
The German mathematician Georg Cantor pioneered set theory and gave us our modern understanding of the mathematics of infinity.
Ali. 2024. “From Countable to Uncountable: The Revolutionary Ideas of the Father of Modern Mathematics, Georg…” Medium. Medium. May 2. https://ali.medium.com/from-countable-to-uncountable-the-revolutionary-ideas-of-the-father-of-modern-mathematics-georg-b7e577141470.
n an era where the spark of wonder seems dimmed by the commonplace nature of discovery and innovation, the story of Georg Cantor emerges as a beacon of enduring enthusiasm and curiosity. Cantor stood as a remarkable exception amid a world growing increasingly indifferent to new insights. This trailblazer of modern mathematics lived his life fueled by an unwavering passion for exploration and understanding.
Ali. “The Father of Infinity and Modern Mathematics: Georg Cantor”. 2022. Medium. https://ali.medium.com/the-father-of-infinity-and-modern-mathematics-georg-cantor-b1d7be15081.
“In mathematics, the art of proposing a question must be held of higher value than solving it.” This analysis belongs to the undervalued genius of his time, Georg Cantor.
Farage, Tim. “How Is It Determined That One Infinite Set Is “Larger” Than Another?”. 2023. Quora. https://qr.ae/przHnm.
One of the most beautiful mathematical facts that are (currently) trivial to a mathematician, but would amaze a layperson is this: “Some infinities are bigger than others”. Ever weirder, given any infinite set, we can create a greater infinite set. This leaves us with this beautiful statement: “Given an infinite set, there is an infinite set with a greater order of infinity.” Incredible.
Marcus du Sautoy argues that mathematics is the driving force behind modern science: Georg Cantor, numbers and infinity.
Merriam, Areeba. “Cantor’s Work in Opposition”. 2022. Medium. https://www.cantorsparadise.com/cantors-work-in-opposition-4a6a7bfc80d0.
Cantor’s work was so profound and whole that within a few decades it became the Lingua Franca of mathematics and the impact it would be going to have on coming generations can not be overestimated. Because “not only did he strengthen already existing foundations for analysis and prove exciting analytic results, but, most significantly, he succeeded in presenting the first outline of a new mathematical discipline, one that would eventually enrich and transform mathematics by forcing it to come to terms with his new theory of the infinite.”
Nagrath, Aditya. “Georg Cantor’s Controversial Career”. 2022. Medium. https://anagrath.medium.com/georg-cantors-controversial-career-c1d2fffe7464.
Georg Cantor was a German mathematician who would eventually be known as a pioneer of “new mathematics.” His work was controversial because it disrupted previously settled matters regarding integer sets. Though it took years for the world to recognize his genius, Cantor’s brilliant methods are now a foundation for modern mathematics. Read on to learn more about this contentious genius.
PolyMaths. “”Some infinities are larger than others”: how to ALWAYS find larger infinities”. 2023. Medium. https://medium.com/@amitai.rosenbaum/some-infinities-are-larger-than-others-how-to-always-find-larger-infinities-3999baeefc70.
You may have heard the bizarre statement that “some infinities are larger than others”. It’s true! But have you ever wondered how we can take one infinity and create another larger one? This article will show how to do precisely that! Also, we’ll go through a fascinating and intuitive proof that this is always possible.
Paul Erdös
Paul Erdős (1913 – 1996) was one of the most productive mathematicians in history. Born in Hungary, he solved countless problems in graph theory, number theory, combinatorics, analysis, probability, and other parts of mathematics. During his life, Erdös published around 1,500 papers and collaborated with more than 500 other mathematicians. In fact, he spent most of his life living out of a suitcase, travelling to seminars, and visiting colleagues!
Labh, Sunny. “Paul Erdős, The Mathematician Of Highest Intellectual Calibre”. 2022. Medium. https://piggsboson.medium.com/paul-erd%C5%91s-the-mathematician-of-highest-intellectual-calibre-825bf30fdf0.
I’ve talked about several mathematicians in my blogs from Maryam Mirzakhani to Terrence tao, from Gottfried Leibniz to Leonhard Euler. I particularly take interest in speaking about mathematicians because they perceive the world and the universe around them in ways that no one else can. Mathematical reasoning unlocks several other areas of your brain and enhances your overall thinking mechanism. This story, however, is about the mathematician who had one of the most incomprehensible personalities of all. His way of living his life and doing mathematics was unique, as mentioned by all his collaborators. I’ve written a separate story about the working ethics of the Hungarian mathematician Paul Erdős, if you haven’t read it you can read it here.
Nagrath, Aditya. “Paul Erdös: Collaborative Mathematics”. 2021. Medium. https://anagrath.medium.com/paul-erd%C3%B6s-collaborative-mathematics-37a04a0d2f3d.
“Paul Erdös – Timeline Of Mathematics – Mathigon”. 2021. Mathigon. https://mathigon.org/timeline/erdos.
Tovey, Craig Aaron. “Who Was The Most Genius Mathematician That You Had Ever Worked With, And What Was The Situation That Made You Think So?”. 2022. Quora. https://qr.ae/pvbEGy.
Paul Erdos. Other mathematicians I have known could, like Erdos, solve problems instantly. Erdos could do more. He would instantly alter your problem to make it a good research question. The first time I talked with him, I asked him two questions. The first was about prime numbers of a certain form. As soon as I finished speaking he answered that my guess was correct and followed as a corollary from a theorem proved 20 years previously. He immediately continued by proposing a generalization that might be true and would be worth exploring. My second question was about Ramsey numbers (part of graph theory). I had conjectured that R(k,m) ≤ R(k−1,m+1) for k>m, which intuitively seemed very plausible to me. Erdos immediately said “That is too hard. Try to prove R(3k,k) ≤ R(2k,2k). That would be very interesting.”
I visualize what Erdos could do as if what is known or readily proved in mathematics is the interior of a ball. Points on the ball’s boundary are the good research problems at the edge of the unknown. Points far from the ball are too difficult for us now. If you gave Erdos a problem inside the ball, he would project it outwards to get a harder version on the boundary that was worthy of research. If you gave Erdos a problem well outside the ball, he would project it inwards onto the ball to give a you a version that you might have a chance of solving. I have not worked with any other mathematician who could do that instantly.
Hilda Geiringer
Hilda Geiringer was the first female lecturer in applied mathematics in history. But not only applied mathematics, but the scope of Hilda’s acquaintance was also much more comprehensive. This Jewish woman was also skilled in applying her knowledge in various fields of science. Geiringer was one of the pioneers of applied mathematics in the twentieth century. At that time, applied mathematics was trying to establish its own uniqueness apart from mathematics. Where Hilda was the most significant contributor, she has also mastered her mathematics in probability and reproduction. Many parts of today’s engineering and science stand based on many of her works. Geiringer took her work more as an emotion than as a profession.
“Hilda Geiringer: The Woman Who Reshaped Mathematics”. 2021. Medium. https://medium.com/@samazgor/hilda-geiringer-the-woman-who-reshaped-mathematics-538b1f1073a.
“Hilda Geiringer – Biography”. 2021. Maths History. https://mathshistory.st-andrews.ac.uk/Biographies/Geiringer/.
“Hilda Geiringer – Wikipedia”. 2021. en.wikipedia.org. https://en.wikipedia.org/wiki/Hilda_Geiringer.
Alexandre Grothendieck
Alexander Grothendieck (28 March 1928 – 13 November 2014) was a German-born mathematician who became the leading figure in the creation of modern algebraic geometry. His research extended the scope of the field and added elements of commutative algebra, homological algebra, sheaf theory, and category theory to its foundations, while his so-called “relative” perspective led to revolutionary advances in many areas of pure mathematics. He is considered by many to be the greatest mathematician of the twentieth century.
“Alexander Grothendieck.” 2024. Wikipedia. Wikimedia Foundation. June 29. https://en.wikipedia.org/wiki/Alexander_Grothendieck.
⭐ Aczel, Amir D. 2006. The Artist and the Mathematician. The Story of Nicolas Bourbaki, the Genius Mathematician Who Never Existed. New York, NY: Thunder’s Mouth Press.
“Alexander Grothendieck and the Search for the Heart of the Mathematical Universe.” 2024. BBC Science Focus Magazine. Accessed July 24. https://www.sciencefocus.com/books/alexander-grothendieck-and-the-search-for-the-heart-of-the-mathematical-universe.
For much of his career he focused on algebraic geometry, and he is credited with the creation of many principles and heuristics used in mathematics today. His work helped mathematicians solve problems that had tormented them for years, including 17th Century mathematician Pierre de Fermat’s Last Theorem. Though revered, he began to withdraw from the mathematical community. He retired in 1988 and removed himself from society, living in solitude until his death in 2014.
“Alexander Grothendieck – Biography.” 2024. Maths History. Accessed July 24. https://mathshistory.st-andrews.ac.uk/Biographies/Grothendieck/.
“Alexander Grothendieck, Permanent Professor from 1958 to 1970.” 2022. IHES. September 9. https://www.ihes.fr/en/professeur/alexander-grothendieck-1/.
Alexander Grothendieck set the framework for modern algebraic geometry, which is now universally adopted. His work was further amplified by Pierre Deligne, originally his disciple, who was recruited to IHES at the age of 26 and is now established at the Institute for Advanced Studies (IAS) in Princeton. Thanks to these new tools, it was possible to bring algebraic geometry and number theory together in a decisive way. He wrote the first four chapters of the famous “Éléments de Géométrie Algébrique” with Jean Dieudonné from 1960 to 1967.
⭐ Artin, Michael, Allyn Jackson, David Mumford, and John Tate. “Alexandre Grothendieck 1928-2014, Part 1” 2024. Notices of the AMS. Volume 63, Number 3, pp 242-255. Accessed July 24. https://www.ams.org/journals/notices/201603/rnoti-p242.pdf.
⭐ Artin, Michael, Allyn Jackson, David Mumford, and John Tate. “Alexandre Grothendieck 1928-2014, Part 2” 2024. Notices of the AMS. April 2016, pp 401-413. Accessed July 24. https://www.ams.org/journals/notices/201603/rnoti-p242.pdf.
In the eyes of many, Alexandre Grothendieck was the most original and most powerful mathematician of the twentieth century. He was also a man with many other passions who did all things his own way, without regard to convention. This is the first part of a two-part obituary; the second part will appear in the April 2016 Notices, The obituary begins here with a brief sketch of Grothendieck’s life, followed by a description of some of his most outstanding work in mathematics. After that, and continuing into the April issue, comes a set of reminiscences by some of the many mathematicians who knew Grothendieck and were influenced by him.
Mumford, David, and John Tate. 2015. “Alexander Grothendieck (1928–2014).” Nature News. Nature Publishing Group. https://www.nature.com/articles/517272a.
Mathematician who rebuilt algebraic geometry. Alexander Grothendieck, who died on 13 November, was considered by many to be the greatest mathematician of the twentieth century. His unique skill was to burrow into an area so deeply that its inner patterns on the most abstract level revealed themselves, and solutions to old problems fell out in straightforward ways.
⭐ “Who Is Alexander Grothendieck?” 2024. Notices of the AMS. Volume 545, Number 8, pp 930-941. Accessed July 24. https://www.ams.org/notices/200808/tx080800930p.pdf.
G. H. Hardy
Godfrey Harold Hardy (1877–1947) was an English mathematician best remembered for his work in analytic number theory and mathematical analysis. He almost single-handedly injected rigour (then a feature limited to continental mathematics) into mainstream British mathematics. But when asked (in an interview with Paul Erdős) to single out his greatest contribution to mathematics, he unreservedly opted for his discovery of Srinivasa Ramanujan, whom he elevated from a clerical position in Madras (modern day Chennai, India) to the elite mathematical stature the genius of Ramanujan richly deserved.
“G. H. Hardy — Rigorous & Shy”. 2020. Medium. https://www.cantorsparadise.com/g-h-hardy-rigorous-shy-8f8afdd689e9.
“BBC Radio 4 Extra – A Brief History Of Mathematics, Hardy And Ramanujan”. 2021. bbc.co.uk. https://www.bbc.co.uk/programmes/b00ss1j4.
Marcus du Sautoy argues that mathematics is the driving force behind modern science: GH Hardy and the prime number ‘menace’.
“G. H. Hardy: Mathematics As Art”. 2021. Medium. https://anagrath.medium.com/g-h-hardy-mathematics-as-art-17ba137dd14a.
David Hilbert
David Hilbert (1862 – 1943) was one of the most influential mathematicians of the 20th century. He worked on almost every area of mathematics, and was particularly interested in building a formal, logical foundation for maths.
Hilbert worked in Göttingen (Germany), where he tutored numerous students who later became famous mathematicians. During the International Congress of Mathematicians in 1900, he presented a list of 23 unsolved problems. These set the course for future research – and four of them are still unsolved today!
“David Hilbert – Timeline Of Mathematics – Mathigon”. 2023. Mathigon. https://mathigon.org/timeline/hilbert.
The first to use the term “abstrakte Hilbertsche Raum” (abstract Hilbert space) was John Von Neumann in his work on Hermitian operators. Von Neumann has the enormous merit of having exploited this powerful tool to give a rigorous reading of Quantum Mechanics (through C*-algebras).
In this regard, a popular story, also cited in the book Mathematical Apocrypha Redux by Steven Krantz, tells that in 1929 John Von Neumann had gone to Göttingen to present his work on Quantum Mechanics, which makes extensive use of the concept of Hilbert space. As at every conference, sitting in the front row, to attend the presentation was none other than Hilbert. When Von Neumann had finished, he was approached by a confused Hilbert, who said:
“Dr. Von Neumann, I am really curious to know what these Hilbert spaces are, after all.”
Alessandro13. “Although he was one of the first mathematicians to elaborate a theory of infinite-dimensional, complete spaces with scalar products, David Hilbert did not know that these, in his honor, had been called ‘Hilbert Spaces’.” 2025. Quora. Accessed February 9. https://qr.ae/pYWBX8.
Sophiya Vasilyevna Kovalevskaya
The first woman to obtain a doctorate (in the modern sense) in mathematics, the first woman appointed to a full professorship in northern Europe and one of the first women to work for a scientific journal as an editor.
“Sofia Kovalevskaya”. 2023. mathwomen.agnesscott.org. https://mathwomen.agnesscott.org/women/kova.htm.
“Sofia Kovalevskaya – Biography”. 2023. Maths History. https://mathshistory.st-andrews.ac.uk/Biographies/Kovalevskaya/.
“Sofia KOVALEVSKY”. 2023. scientificwomen.net. https://scientificwomen.net/women/kovalevsky-sofia-50.
“Sofya Kovalevskaya – Wikipedia”. 2023. en.wikipedia.org. https://en.wikipedia.org/wiki/Sofya_Kovalevskaya.
Sophiya Vasilyevna Kovalevskaya
A pioneering mathematician during a time when women had limited access to higher education.
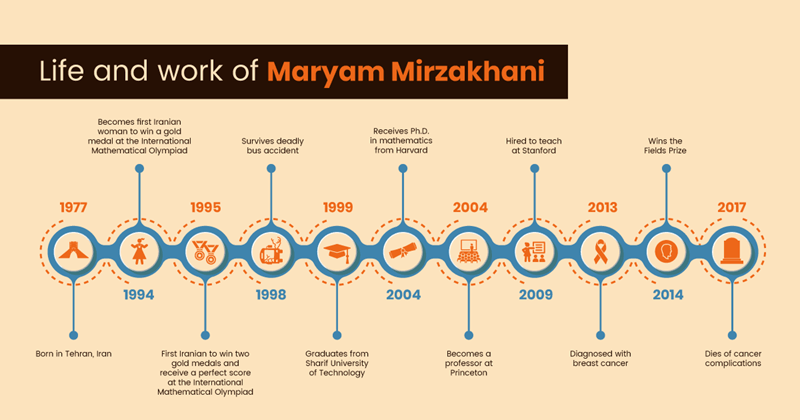
Maryam Mirzakhani
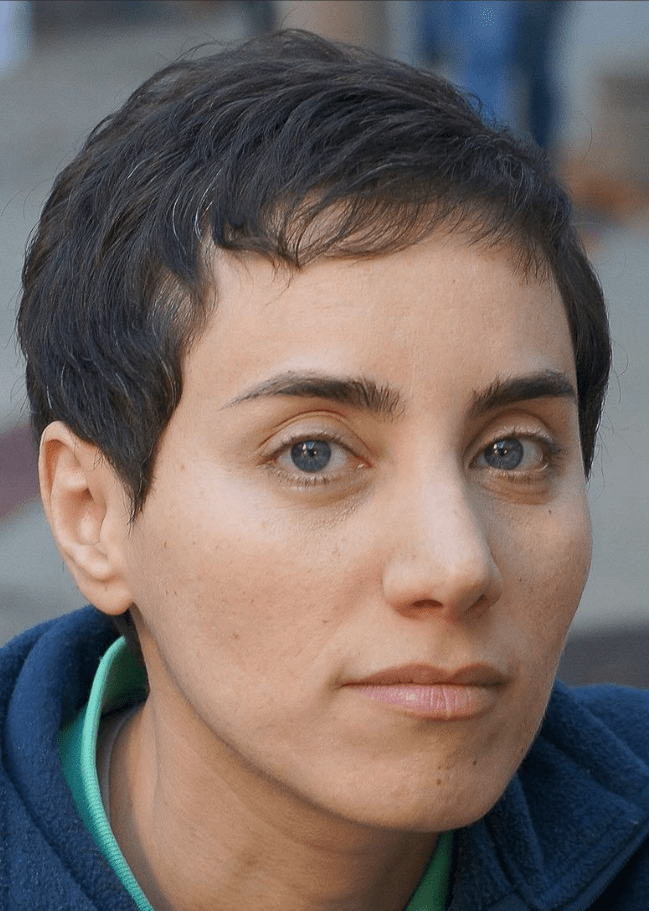
Maryam Mirzakhani, (born May 3, 1977, Tehrān, Iran—died July 14, 2017, Palo Alto, California, U.S.), Iranian mathematician who became (2014) the first woman and the first Iranian to be awarded a Fields Medal. The citation for her award recognized “her outstanding contributions to the dynamics and geometry of Riemann surfaces and their moduli spaces.”
The Fields Medal, often described as the mathematician’s Nobel Prize, is given every four years to no more than four mathematicians, all of whom are 40 or younger. She was named for her work on complex geometry and dynamic systems.
Ms. Mirzakhani, of Iran, received the award in Seoul, South Korea, in 2014. “This is a great honor. I will be happy if it encourages young female scientists and mathematicians,” she said at the time. “I am sure there will be many more women winning this kind of award in coming years.”
Ms. Mirzakhani — known for taking the difficult, complicated path to solve mathematical problems — studied the symmetry of curved surfaces and other theoretical concepts known as “pure mathematics.”
“Maryam Mirzakhani: First Woman to Win Math’s Nobel Prize | Elephant Learning”. 2023. Elephantlearning.Com. https://www.elephantlearning.com/post/maryam-mirzakhani-first-woman-to-win-maths-nobel-prize.
Ali. “9 Inspirational Women in Math: Meet the Pioneers Who Paved the Way”. 2023. Medium. https://ali.medium.com/9-inspirational-women-in-math-meet-the-pioneers-who-paved-the-way-b9334e5c8895.
What made Mirzakhani’s work so groundbreaking was her ability to connect complex ideas from different fields in mathematics. Her unique approach to problem-solving involved creative thinking and visualizing mathematical concepts in new ways. She was able to use her deep understanding of mathematical structures to develop innovative methods that other mathematicians around the world later adopted.
“Maryam Mirzakhani – Wikipedia”. 2023. en.wikipedia.org. https://en.wikipedia.org/wiki/Maryam_Mirzakhani.
Howlett, Joseph. 2025. “Years After the Early Death of a Math Genius, Her Ideas Gain New Life.” Quanta Magazine. March 3. https://www.quantamagazine.org/years-after-the-early-death-of-a-math-genius-her-ideas-gain-new-life-20250303/.
Her earliest work dealt with “hyperbolic” surfaces. On such a surface, parallel lines arc away from each other rather than staying the same distance apart, and at every point, the surface curves in two opposing directions like a saddle. Although we can picture the surface of a sphere or doughnut, hyperbolic surfaces have such strange geometric properties that they’re impossible to visualize. But they’re also important to understand, because such surfaces are ubiquitous in mathematics and even string theory.
Mirzakhani was an influential cartographer of the hyperbolic universe. While still in graduate school, she developed groundbreaking techniques that allowed her to start cataloging these shapes, before moving on to revolutionize other areas of mathematical research. She hoped to revisit her map of the hyperbolic realm at a later date — to fill in its details and make new discoveries. But before she could do so, she was diagnosed with breast cancer. She died in 2017, just 40 years old.
Two mathematicians have since picked up the thread of her work and spun it into an even deeper understanding of hyperbolic surfaces. In a paper posted online last month, Nalini Anantharaman of the Collège de France and Laura Monk of the University of Bristol have built on Mirzakhani’s research to prove a sweeping statement about typical hyperbolic surfaces. They have shown that surfaces once thought to be rare, if not impossible, are actually common. In fact, if you were to pick a hyperbolic surface at random, it essentially would be guaranteed to have certain critical properties.
Klarreich, Erica. 2019. “A Tenacious Explorer of Abstract Surfaces.” Quanta Magazine. https://www.quantamagazine.org/maryam-mirzakhani-is-first-woman-fields-medalist-20140812/.
Mirzakhani — a 37-year-old mathematics professor at Stanford University — still writes elaborate stories in her mind. The high ambitions haven’t changed, but the protagonists have: They are hyperbolic surfaces, moduli spaces and dynamical systems. In a way, she said, mathematics research feels like writing a novel. “There are different characters, and you are getting to know them better,” she said. “Things evolve, and then you look back at a character, and it’s completely different from your first impression.”
The Iranian mathematician follows her characters wherever they take her, along story lines that often take years to unfold. Petite but indomitable, Mirzakhani has a reputation among mathematicians for tackling the most difficult questions in her field with dogged persistence. “She has a fearless ambition when it comes to mathematics,” said Curtis McMullen of Harvard University, who was Mirzakhani’s doctoral adviser.
University, Stanford. 2017. “Maryam Mirzakhani, Mathematician And Fields Medal Winner, Dies At Stanford | Stanford News”. Stanford News. https://news.stanford.edu/2017/07/15/maryam-mirzakhani-stanford-mathematician-and-fields-medal-winner-dies/.
“Maryam MIRZAKHANI”. 2023. scientificwomen.net. https://scientificwomen.net/women/mirzakhani-maryam-69.
“A Tenacious Explorer Of Abstract Surfaces | Quanta Magazine”. 2014. Quanta Magazine. https://www.quantamagazine.org/maryam-mirzakhani-is-first-woman-fields-medalist-20140812/.
“Maryam Mirzakhani – Biography”. 2023. Maths History. https://mathshistory.st-andrews.ac.uk/Biographies/Mirzakhani/.
“What Were Maryam Mirzakhani’s Greatest Contributions To Mathematics?”. 2023. Quora. https://www.quora.com/What-were-Maryam-Mirzakhanis-greatest-contributions-to-Mathematics/.
Emmy Noether
“Emmy Noether – Wikipedia”. 2020. en.wikipedia.org. https://en.wikipedia.org/wiki/Emmy_Noether.
Amalie Emmy Noether (23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She discovered Noether’s theorem, which is fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed some theories of rings, fields, and algebras. In physics, Noether’s theorem explains the connection between symmetry and conservation laws.
“Five Fast Facts About Mathematician Emmy Noether”. 2021. energy.gov. https://www.energy.gov/articles/five-fast-facts-about-mathematician-emmy-noether.
Scientists, Top, and List Scientists. 2021. “Emmy Noether – Biography, Facts And Pictures”. famousscientists.org. https://www.famousscientists.org/emmy-noether/.
“The Most Important Woman In 20th-Century Mathematics: Emmy Noether”. 2021. Medium. https://anagrath.medium.com/?p=1e3ad8ce499e.
Who did Albert Einstein regard as the most important woman in mathematics? That honor goes to Emmy Noether, a prolific mathematician, and physicist working in the early 20th-century. Besides working in a male-dominated field and fighting for recognition at every turn, Emmy also had to contend with the turmoil and chaos of the Nazi takeover in Germany. As a Jewish woman in academia, she was a high-profile target for the Nazi party. Although she successfully escaped Germany and came to America, many of her colleagues and family members were not so lucky. Emmy Noether’s life is an empowering and illuminating example of someone who loves what they do so much that they persevere despite nearly insurmountable obstacles.
Pincha, Yash. “She Who Changed Physics Forever”. 2022. Medium. https://medium.com/quantafy/she-who-changed-physics-forever-c508a46c5bf7.
Noether’s theorem, postulated by Amalie Emmy Noether, is by far, one of the most beautiful mathematical ideas out there. It doesn’t receive nearly as much credit as it deserves.
Ramszay, Keith. “Who Was the Most Famous Mathematical Female Genius?” 2024. Quora. Accessed June 9. https://qr.ae/psxBn2.
I think Emmy Noether wins here. Fame is not always handed out fairly, of course, but it’s hard to think of many people of either sex who are more deserving of fame. When she died the New York Times had an obituary titled something like “Bryn Mawr prof. dies”. Einstein and Weyl told them that when the world’s greatest algebraist dies, she deserves a bit more. Here is a brief obituary by Einstein: NY Times obituary.
Another algebraist gave lectures on her work without being clear enough on who did what, but nowadays it’s clear that she is the real pioneer. One of the key concepts in commutative algebra is the “Noetherian ring”, a ring in which each increasing chain of ideals eventually stabilizes. That property in itself is behind so much of what people now do in commutative algebra, and in algebraic geometry (which in general depends a lot on commutative algebra).
Many people who have heard of her have heard of her because of her work in physics, and probably are unaware of all that work in algebra. Just think, work in two areas, each of which is separately worth making someone famous! Ground-breaking work in both areas. As the bio by Einstein points out, she deserved much better career success than she was allowed to have. She also accomplished all this in spite of not living especially long (53).
Hypatia probably is one of the most famous women mathematicians, but it isn’t so much because of her mathematics that she is famous. I would say she was more of a philosopher or public figure, who like many people with some breadth of interests also did some mathematics.
What is the most beautiful theorem in physics?
In my opinion, Noether’s theorem.
Not only is it the most beautiful theorem but it’s also one of the most important. It’s utilized in classical mechanics, classical field theory, quantum mechanics, and quantum field theory. It was proved by Emmy Noether, one of the most badass women ever.
The theorem states, “if a system has continuous symmetry, then there is a corresponding quantity whose values are conserved over a period of time.” In other words, Noether’s theorem establishes a link between continuous symmetries and conservation laws.
[Mathematical Proof]
In modern physics, you will find symmetries everywhere. They let you obtain conservation laws without the need of specifying the law as an axiom.
Some symmetries and their conservation laws include:
- Time-invariance →→ Energy
- Rotational symmetry →→ Angular momentum
- Phase shifts →→ Conservation of charge
Dwight Neuenschwander’s book Emmy Noether’s Wonderful Theorem goes into far more detail.
Elseweifi, Amr. “What Is The Most Beautiful Theorem In Physics?” 2022. Quora. https://qr.ae/pvbERD.
Henri Poincaré
TBS
Who is more influential in mathematics, Henri Poincaré or Albert Einstein?
This is a fun question. The answer is “Henri Poincaré” by an almost ridiculous margin.
Poincaré and Einstein were contemporaries: Poincaré was born in 1854; Einstein was born in 1879. Both of these men did early pioneering work in special relativity. Of the two of them, Einstein is undoubtedly more famous.
Einstein was also undoubtedly the more important physicist. (Although Poincaré was nominated for a Nobel Prize in Physics many, many times. In 1910, there were 58 nominations for the prize and 34 of them named Poincaré.)
Einstein can even be said to have had some limited influence in mathematics: he created Einstein notation for tensors (although that has been used more by physicists than mathematicians), his paper on Brownian motion helped inspire later development of the Wiener process, and his ideas around general relativity pushed mathematicians to delve deeper into pseudo-Riemannian manifolds.
But, as a mathematician, Einstein is as to Poincaré—The Last Universalist—as that kid round the block who’s pretty good at shooting hoops is to Michael Jordan. It’s almost unfair to compare them; they’re barely playing the same sport.
(An aside: I usually don’t like questions like this. Most variants of it asked by the QPG are utterly banal. But this was a question I could genuinely see real people having, and it is a great excuse to talk about one of the greatest mathematicians to have ever lived. What’s not to love?)
So who was Henri Poincaré? Why is he considered one of the greatest mathematicians? Why is he called “The Last Universalist”?
Jules Henri Poincaré was born to an influential French family in 1854. He was a polymath; in school, he excelled in all of his subjects but was particularly gifted in mathematics. He earned a doctoral degree studying under Charles Hermite (himself a mathematical giant) in 1879 and very quickly established himself as one of the greatest mathematicians of the era.
What was it that Poincaré worked on? Everything.
Over the course of his life, Poincaré quite literally made contributions in every field of mathematics that existed at that time and established a fair few more.
For example, Poincaré’s earliest work was in partial differential equations, which is what his doctoral thesis was on. There were already many known techniques for solving various families of PDEs, such as Fourier series, separation of variables, Lie groups, etc., etc. But what Poincaré recognized was that
- there was no hope of finding anything like a closed form solution for most PDEs, but
- you could study the geometric properties of the solutions and extract information about their overall behavior even without this.
In so doing, Poincaré invented—and gave many of the foundational results for—the qualitative theory of differential equations, applicable to both ODEs and PDEs. He then immediately turned to seeing how this theory could be applied to many problems in physics. In 1887, Oscar II (the King of Sweden) established a prize for whoever could find a solution to the three-body problem—that is, could give some kind of “closed form” description for the paths of three bodies orbiting each other.
An illustration of one such possible orbit. Created originally by WikiMedia user MaxwellMolecule.
In 1889, Poincaré won the prize—not because he had solved the problem, but he had shown just how absurdly difficult it was. (The problem was actually solved as stated by Karl Sundman in 1912, but his solution is in some sense completely useless: you can use it to predict the orbits, but you need so an overwhelming amount of computational power to do it that you are better off just using numerical approximations.) To quote Karl Weierstrass, who was one of the judges (and another titan of mathematics):
This work cannot indeed be considered as furnishing the complete solution of the question proposed, but that it is nevertheless of such importance that its publication will inaugurate a new era in the history of celestial mechanics.
If anything, he was underselling it: Poincaré’s work had many of the important ideas that eventually led to the birth of chaos theory
These discoveries alone would have been enough to secure Poincaré a place in mathematical history. But he did much, much more. To give some highlights:
- He effectively created the field of algebraic topology, introducing the fundamental group, Betti numbers, and so on.
- He was the first one to show the importance of groups in physics, and in particular investigated what is now known as the Poincaré group.
- He defined what is now known as Poincaré series, a type of modular form. In the modern era, modular forms are of crucial importance in number theory, where they give analytic tools for answering questions about things like partitions.
There was no area of mathematics that existed at that time that Poincaré did not touch at some point. And, really, he is probably the last mathematician of whom that can be said: in the 20th century there was such an explosion of mathematical discovery that it is no longer humanly possible to do what Poincaré did. It is for this reason that he is known as the Last Universalist.
Sheydvasser, Senia. “Who is more influential in mathematics, Henri Poincaré or Albert Einstein? – Quora”. 2023. Quora. https://qr.ae/prEE5u.
Srinivasa Ramanujan
An Indian mathematician with least resource and great intelligence who lived on earth for very short period of time. Ramanujan was born on 22 Dec, 1887 in Tamil Brahmin Iyengar family, in Erode. He grew up in very religious thoughts, beliefs, but despite that passion towards mathematics was flourished since childhoods days. He was the prodigy, he was able to understand and solve mathematics well above his age. At age of 16 he got his mind at A Synopsis of Elementary Results in Pure and Applied Mathematics, a collection of 5000+ theorems, which lead him to develop Bernoulli Numbers independently. From then he did mathematics of his own, and independently rediscovers many known mathematics facts. Some of which he sent to GH Hardy, for which Hardy was impressed and his professional mathematician career started.
“Ramanujan”. 2020. Medium. https://medium.com/maths163/ramanujan-48b6c56c199d.
“BBC Radio 4 Extra – A Brief History Of Mathematics, Hardy And Ramanujan”. 2021. bbc.co.uk. https://www.bbc.co.uk/programmes/b00ss1j4.
Marcus du Sautoy argues that mathematics is the driving force behind modern science: GH Hardy and the prime number ‘menace’.
Cepelewicz, Jordana, Erica Klarreich, Matt von Hippel, Gregory Barber, and substantive Quanta Magazine moderates comments to facilitate an informed. 2024. “Srinivasa Ramanujan Was a Genius. Math Is Still Catching Up.” Quanta Magazine. October 21. https://www.quantamagazine.org/srinivasa-ramanujan-was-a-genius-math-is-still-catching-up-20241021/.
One afternoon in January 2011, Hussein Mourtada leapt onto his desk and started dancing. He wasn’t alone: Some of the graduate students who shared his Paris office were there, too. But he didn’t care. The mathematician realized that he could finally confirm a sneaking suspicion he’d first had while writing his doctoral dissertation, which he’d finished a few months earlier. He’d been studying special points, called singularities, where curves cross themselves or come to sharp turns. Now he had unexpectedly found what he’d been looking for, a way to prove that these singularities had a surprisingly deep underlying structure. Hidden within that structure were mysterious mathematical statements first written down a century earlier by a young Indian mathematician named Srinivasa Ramanujan. They had come to him in a dream.
Sharma, Ashwin. “Lessons From A Self-Taught Mathematical Genius Who Succeeded Against All Odds”. 2022. Medium. https://medium.com/@ash.sharma3_14/lessons-from-a-self-taught-mathematical-genius-who-succeeded-against-all-odds-62fa50057279.
Srinivasa Ramanuja’s life is the most romantic story in science. His story is one of succeeding against all odds. A self-taught mathematical genius living in extreme poverty in South India became one of the greatest mathematicians of the 20th century. Despite being a two-time college dropout, he revolutionized the field of number theory and became the first Indian to be elected fellow of the Royal Society in England in 1918. His life was tragically cut short at the age of 32. His short, but brilliant life, is a testament to living life at the very frontiers of human discovery. Intertwined in Ramanujan’s incredible biography are three of the most important lessons we can learn from his life.
Ramanujan was a self-taught Indian mathematician who travelled to England to work with professor G H Hardy after sending him a letter describing some of his remarkable ideas. In this video we take a look at that letter and at Hardy’s initial response.
Bernhard Riemann
Bernhard Riemann (1826 – 1866) was a German mathematician working in the fields of analysis and number theory. He came up with the first rigorous definition of integration, studied differential geometry which laid the foundation for general relativity, and made groundbreaking discoveries regarding the distribution of prime numbers.
“Bernhard Riemann – Timeline Of Mathematics – Mathigon”. 2022. Mathigon. https://mathigon.org/timeline/riemann.
Mancuso, Olivia. “Bernhard Riemann: Shy, Brilliant, Revolutionary”. 2022. Medium. https://anagrath.medium.com/bernhard-riemann-shy-brilliant-revolutionary-773226ae3002.
Bernhard Riemann (1826–1866) was a shy German mathematician known for his fear of public speaking and the brilliant journey to overcome it. He became a mathematics professor after presenting a habilitation thesis on multidimensional spaces. His contributions to mathematics include Riemannian Geometry, which profoundly impacted Einstein’s theory of relativity. Read on to learn about this prolific German mathematician!
“The Distribution Of Primes – Divisibility And Primes – Mathigon”. 2022. Mathigon. https://mathigon.org/course/divisibility/distribution-of-primes#riemann.
When only 15 years old, the German mathematician Carl Friedrich Gauss ad a groundbreaking new idea: he counted the number of primes up to a certain point, and showed the results in a chart (see The Riemann Hypothesis on the The Distribution of Primes page for the interactive chart). Along the x-axis you can see all integers. Whenever there is a prime, the Prime Counting Function increases by one. As we zoom out, the blue line becomes very smooth. Gauss noticed that the shape of this function looks very similar to the function x/log(x). He predicted that the two functions are always “approximately similar”, and this was proven in 1896. However, there is still a significant error between the actual number of primes, and Gauss’s approximation. In 1859, the mathematician Bernhard Riemann discovered an approximation that looked much better, but he wasn’t able to prove that it would always work. His idea became known as the Riemann Hypothesis.
“Bernhard Riemann – Wikipedia”. 2020. en.wikipedia.org. https://en.wikipedia.org/wiki/Bernhard_Riemann.
Georg Friedrich Bernhard Riemann (17 September 1826 – 20 July 1866) was a German mathematician who made contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the first rigorous formulation of the integral, the Riemann integral, and his work on Fourier series. His contributions to complex analysis include most notably the introduction of Riemann surfaces, breaking new ground in a natural, geometric treatment of complex analysis. His 1859 paper on the prime-counting function, containing the original statement of the Riemann hypothesis, is regarded as one of the most influential papers in analytic number theory. Through his pioneering contributions to differential geometry, Riemann laid the foundations of the mathematics of general relativity. He is considered by many to be one of the greatest mathematicians of all time.
“Bernhard Riemann – Biography, Facts And Pictures”. 2022. famousscientists.org. https://www.famousscientists.org/bernhard-riemann/.
Bernhard Riemann made profound, far-sighted discoveries with lasting consequences for mathematics and our understanding of space, gravity, and time. Riemannian geometry completely reformed the field of geometry and became the mathematical foundation of Einstein’s general theory of relativity. Finding a proof or disproof of the Riemann hypothesis continues to be the greatest, deepest, unsolved problem in number theory – the search for a solution has become the holy grail of mathematics. Another of Riemann’s innovations, Riemann surfaces, made a strong link between topology and complex function theory. Riemann was the first person to rigorously define the integral.
John von Neumann
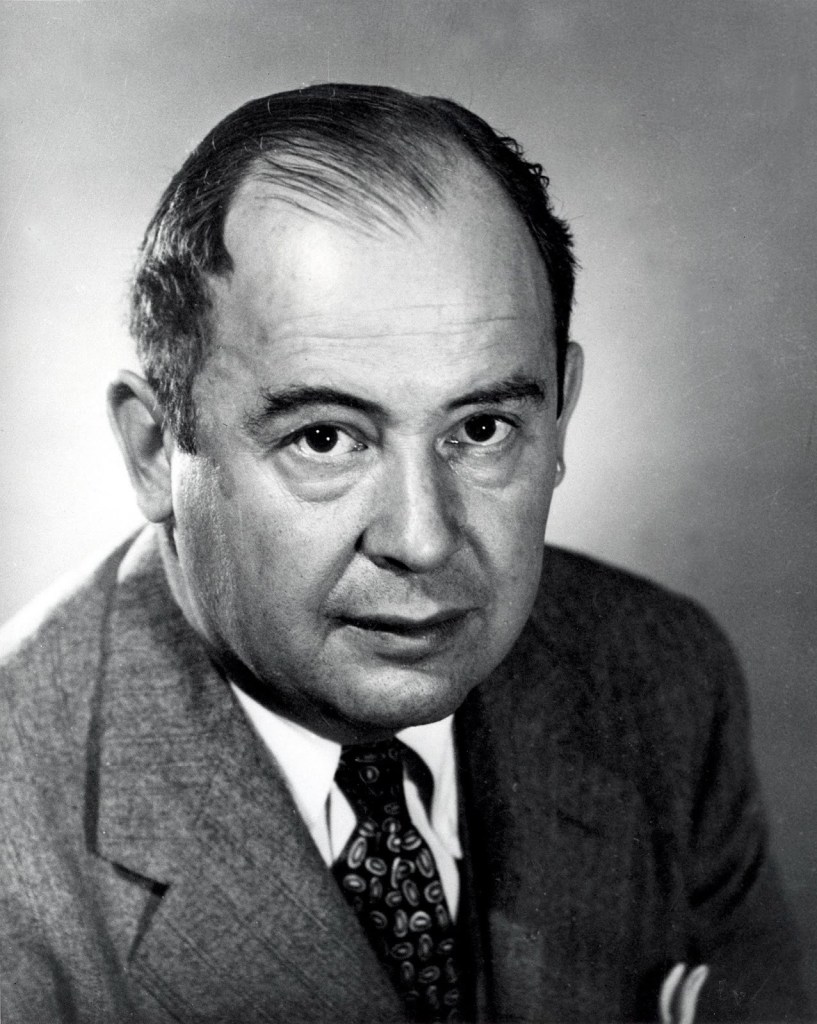
John von Neumann (1903 – 1957) was a Hungarian-American mathematician, physicist and computer scientist. He made important contributions to pure mathematics, was a pioneer of quantum mechanics, and developed concepts like game theory, cellular automata, self-replicating machines, and linear programming.
During World War II, von Neumann was a key member of the Manhattan Project, working on the development of the hydrogen bomb. He later consulted for the Atomic Energy Commission and the US Air Force.
“John Von Neumann: The Colorful Mathematician Who Helped Design The Atomic Bomb”. 2022. Medium. https://anagrath.medium.com/john-von-neumann-the-colorful-mathematician-who-helped-design-the-atomic-bomb-f36576272881.
John von Neumann was a Hungarian child prodigy turned famous mathematician known for memorizing entire books, computing complex equations in his head, and having an animated personality.
He lived an eccentric lifestyle filled with frequent parties and loud music — but also was responsible for many critical military contributions in World War II. Von Neumann was truly a fascinating mathematician whose impressive resume could only be topped by his “off-color” sense of humor and zest for life.
“John Von Neumann – Wikipedia”. 2022. en.wikipedia.org. https://en.wikipedia.org/wiki/John_von_Neumann.
John von Neumann (December 28, 1903 – February 8, 1957) was a Hungarian-American mathematician, physicist, computer scientist, engineer and polymath. Von Neumann was regarded as perhaps the mathematician with the widest coverage of the subject in his time and was said to have been “the last representative of the great mathematicians who were equally at home in pure and applied mathematics”. He integrated pure and applied sciences.
“John Von Neumann – Biography, Facts And Pictures”. 2022. famousscientists.org. https://www.famousscientists.org/john-von-neumann/.
John Von Neumann was a polymath and pioneer of the application of operator theory to quantum mechanics, in the development of functional analysis. Along with fellow physicists Edward Teller and Stanislaw Ulam, von Neumann worked out key steps in the nuclear physics involving thermonuclear reactions and the hydrogen bomb.
Von Neumann wrote 150 published papers in his life; 60 in pure mathematics, 20 in physics, and 60 in applied mathematics.
His last work, published in 1958 “The Computer and the Brain”, explores the analogies between computing machines and the living human brain.
Thorbjørnsen, Gylve. “Who Is The Smartest Person Who Has Ever Lived? Was It Plato, Aristotle, Newton, Einstein Or Somebody Else? – Quora”. 2022. quora.com. https://qr.ae/pvHQr9.
This guy, to me at least seems like a genius. He was smart as hell, really knowledgeable and it was just purely insane.
He was one of the worlds most prolific mathematicians. His research helps in so many fields. He was also known to be able to recite entire books out of memory that he had read years beforehand.
I’m too lazy to write them in myself so here is quotes from him and about him from himself, and some extremely intelligent gents 😉
- When von Neumann graduated from gymnasium (high school) he knew so much math that the university let him skip all of undergraduate mathematics and go straight to a PhD.
- George Polya was giving advanced lecture at Zurich. He came to a certain conjecture and said that there is no known proof and the proof was likely to be difficult. After 5 minutes, von Neumann raised his hand and, when Polya called on him, he came to the board and wrote a proof. “From that moment” Polya said “I was scared of von Neumann.”
- Edward Teller (who won a Nobel prize and was no slouch) said “von Neumann would carry on a conversation with my 3-year-old son, and the two of them would talk as equals, and I sometimes wondered if he used the same principle when he talked to the rest of us.”
- Another Nobelist, Hans Bethe, said “I have sometimes wondered whether a brain like von Neumann’s does not indicate a species superior to that of man”.
Peter. “John Von Neumann was highly talented, but should he really be considered a highly accomplished mathematician?”. 2023. Quora. https://qr.ae/pyoN55.
Von Neumann made major contributions to many fields, including mathematics (mathematical logic, measure theory, functional analysis, ergodic theory, group theory, lattice theory, representation theory, operator algebras, matrix theory, geometry, and numerical analysis), physics (quantum mechanics, hydrodynamics & ballistics, nuclear physics and quantum statistical mechanics), economics (game theory and general equilibrium theory), computing (Von Neumann architecture, linear programming, numerical meteorology, scientific computing, self-replicating machines, stochastic computing), and statistics.
Alon, Amit. “John Von Neumann was highly talented, but should he really be considered a highly accomplished mathematician?”. 2023. Quora. https://qr.ae/pyoNbC.
Gifted from an early age with an extraordinary memory and ability in mental calculations, a gift that would accompany him until the end of his days, Von Neumann was also a polyglot: at the age of six he loved to converse with his father in Greek and Latin. He also seemed capable of repeating entire sentences, if not pages, from books he had read years before.
Alessandro13. “Among the Greatest Mathematicians and Physicists of the Last Century, There Is without a Doubt John Von Neumann.” 2025. Quora. Accessed February 9. https://qr.ae/pYW3iz.
Medium Member Only
⭐ I suggest that you read the entire reference. Other references can be read in their entirety but I leave that up to you.
Mathematical Mysteries 