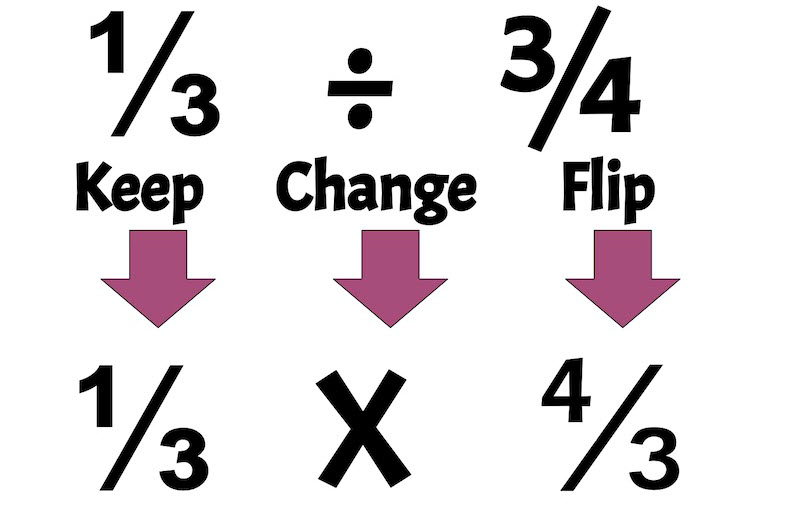Keep, Change, Flip

“Keep, Change, Flip” (KCF) is a mnemonic for dividing fractions: Keep the first fraction, Change the division sign to multiplication, and Flip (find the reciprocal of) the second fraction, then multiply as usual. This method simplifies dividing by a fraction into multiplying by its reciprocal, making the problem solvable by standard multiplication.

Example

$\frac{2}{7}\div \frac{3}{5}$

Keep: 2/7
Change: ÷ to ×
Flip: 3/5 to 5/3
Multiply

$\frac{2}{7}\times \frac{5}{3}\,\,=\,\,\frac{10}{21}$

Why Does KCF Work?

Division by a fraction is multiplying by its reciprocal. Here’s how to derive it:

Recall the definition of division:

$a\,\,\div \,\,b\,\,=\,\,a\,\,\times \,\,\frac{1}{b}$

This holds for any numbers, including fractions.

Reciprocal of a fraction:

The reciprocal of r/s (where r ≠ 0 and s ≠ 0 ) is s/r, because

$\frac{r}{s}\,\,\times \,\,\frac{s}{r}\,\,=\,\,\frac{r\,\,\cdot \,\,s}{s\,\,\cdot \,\,r}\,\,=\,\,1$

$\frac{1}{\frac{r}{s}}\,\,=\,\,\frac{s}{r}$

Apply to fractions:

Let the first fraction be p/q and the second be r/s. Then:

$\frac{p}{q}\,\,\div \,\,\frac{r}{s}\,\,=\,\,\frac{p}{q}\,\,\times \,\,\frac{1}{\frac{r}{s}}\,\,=\,\,\frac{p}{q}\,\,\times \,\,\frac{s}{r}$

This is exactly keep p/q, change ÷ to ×, flip r/s to s/r.

Visual Confirmation

Imagine dividing a pizza as follows: 3/4 of a pizza ÷ 2/5 pizza per slice = how many slices?

Using keep, change flip, we see that it is equivalent to 3/4 of a pizza × 5/2 slices per pizza = 15/8 slices or

$1\frac{7}{8}\,\,slices$

How many slices of size two-fifths can be obtained from three-fourths of a pizza? We can see this visually in the fraction chart below, and using the following process.

Cut the pizza into fourths (green).
Show two-fifths in relation to three-fourths (yellow).
Show two-fifths divided into eighths since we are trying to visualize fifteen-eights (using the orange gradient) and subsequently seven-eights (using the black hatching).
Note that we can get one (of size two-fifths) and seven-eighths (of two-fifths) of a slice from three-fourths of a pizza.

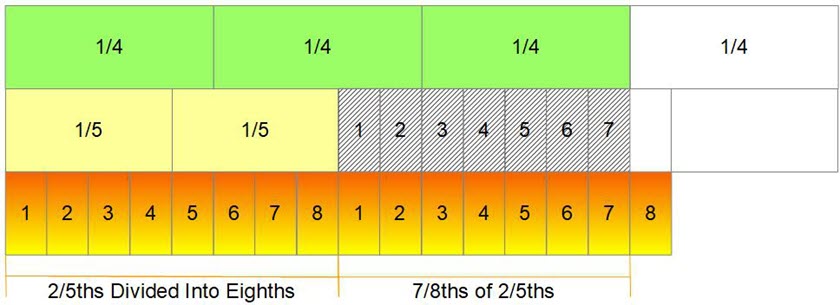
*Fraction chart showing how many slices of size two-fifths*
*can be obtained from three-fourths of a pizza*.

This rule relies on fraction multiplication properties and the multiplicative inverse, making it universal for nonzero fractions.