A percentage is a different way of representing fractions or decimals. It represents part of a whole thing that is in question. But instead of leaving the result as a fraction or as a decimal, it is expressed as a percentage. In other words, a percentage means out of 100, where 100 is the whole thing or a complete section. How do you know that a value is in percentage? Usually, the symbol % accompanies the value. An example of value and sign notation is 23%. [1]
There are three basic types of percent problems: [6]
- Find a given percent of a given number.
- Find a percent given two numbers.
- Find a number that is a given percent of another number. For example, 10% of what number is 12?
Percentage

Example 1
What is 80% of 200?
In this problem, of = 200, is = ?, and % = 80
We get:
is/200 = 80/100
Since is is an unknown, you can replace it by y to make the problem more familiar.
y/200 = 80/100
Cross multiply to get y × 100 = 200 × 80
y × 100 = 16000
Divide 16000 by 100 to get y
Since 16000/100 = 160, y = 160
So, 80% of 200 is 160
Example 2
For example, 15 is what percent of 50?
In this problem, of = 50, is = 15, and % = ?
We get:
15/50 = ?/100
Since the percentage is an unknown, you can replace it by y to make the problem more familiar.
15/50 = y/100
Cross multiply to get y × 50 = 15 × 100
y × 50 = 1500
Divide 1500 by 50 to get y
Since 1500/50 = 30, y = 30
So, 15 is 30% of 50
Example 3
30 is 20% of what number?
In this problem, of = ?, is = 30, and % = 20
We get:
30/? = 20/100
Since of in an unknown, you can replace it by y to make the problem more familiar.
30/y = 20/100
Cross multiply to get 30 × 100 = 20 × y
y × 20 = 3000
Divide 3000 by 20 to get y
Since 3000/20 = 150, y = 150
So, 30 is 20% of 150
Below, we show three more examples to calculate 30% of 500 similar to what we learned above.
- Start with the percentage formula. Calculate how many times 100 must be multiplied by to get 500 (i.e., 5) in the denominator, then multiply the numerator and denominator by 5 to obtain the value for t (i.e., the value of the numerator).
- Like the percentage formula, we cross multiply and establish an algebraic equation and solve for t.
- Multiply 500 by 30% (0.30 or 30/100) to get the percentage.

Is there any difference in each of the methods above? No really. They are different means to calculate a percentage.
Percentage is a special case of proportion. Proportion is just any positive fraction while percentage has a fixed denominator equal to 100. Both proportion and percentage can be written as fractions. The percentage is out of 100. The proportion is out of any given total.
The following figures show graphically how a percentage is also the slope of a line using 20% (m = 20/100) as an example.
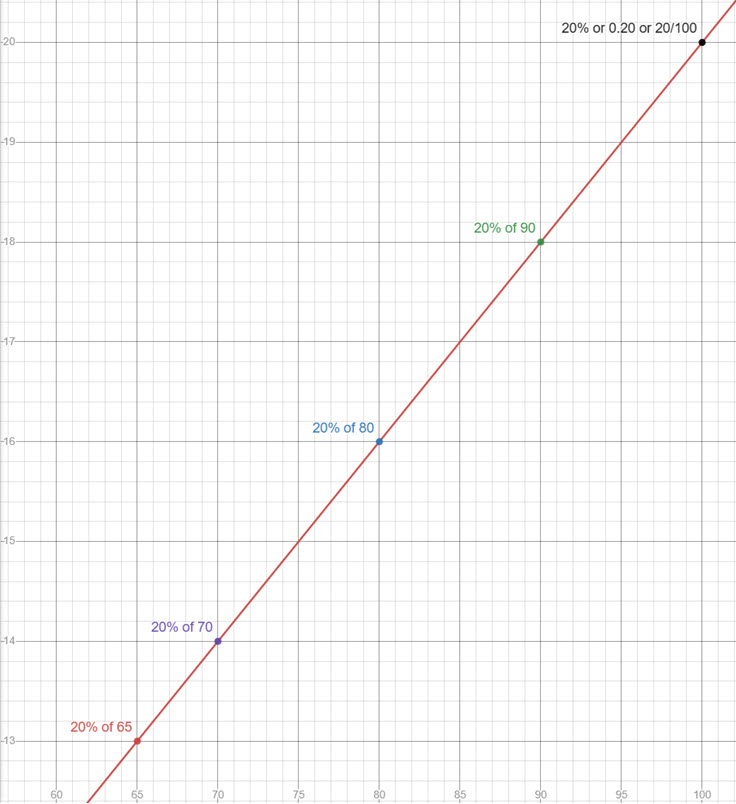

Percentages Are Reversable
Percentages are always reversible. For example, 25% of 8 = 8% of 25, will that always be true no matter what the numbers are.
This is true because of the commutative property of multiplication: a x b = b x a.
Percentage Difference
Percentage difference tells us the measurement of two different experimental values where one value is higher. In other words, the percentage difference is defined as the absolute value of the ratio of the difference between two numbers and their average, expressed as a percentage. For example, if we need to determine the percentage of customers in April over the number of customers in May, the percent difference formula will be used. Let us look at the percent difference between two numbers and the steps to calculate the same. [5]
Percentage Difference is used when both values mean the same thing. For example, the heights of two people. It should NOT be used when there is an initial value or a final value.
See the K-12 – Percentage Difference webpage for a detailed explanation of the percentage difference.
Percentage Difference Between Two Numbers
The percentage difference between two numbers is the method to calculate the difference between any two values in terms of the percentage of the average of both the values. It is used when the quantities are of the same kind, for example, numbers of cars sold in January and February, heights of Ron and Harry, the weight of two objects, etc. While calculating the percent difference between two numbers, we take the average value of both as a reference value. The average is calculated by dividing the sum of both numbers by the total number of quantities taken. Let us find the percentage difference of 10 and 32. [5]
Difference of 10 and 32 = 32 – 10 = 22
Average of 10 and 32 = (10 + 32)/2 = 42/2 = 21
Percent difference = 22/21 × 100 = 104.76%
Percentage Difference vs Percentage Change
Percentage difference and percentage change are two concepts that people often end up using interchangeably but they are different from each other. Listed below are a few differences between percentage difference and percentage change. [5]
| Percentage Difference | Percentage Change |
|---|---|
| It is the percentage of the ratio of the difference between two values and the average of two values, where one value is higher or lower than the second value. | It is the difference between two values as a percentage of one or both values where the old value is compared to the new value or vice-versa. |
| While calculating the percentage difference, the difference between both values is divided by the average of the two values. | While calculating the percentage change, the difference between both values is divided by the old value. |
| If the derived answer is negative, the minus sign must be ignored, and the value must be taken as it is. | If the derived answer is negative, the negative value shows a decrease, whereas a positive value shows an increase. |
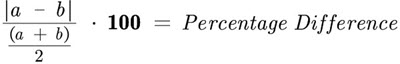 | 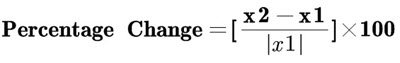 |
Common Uses of Percentages
A percentage is a number that represents the fractional part out of 100 (per cent literally means per one hundred). Thus 87% means 87/100 or 0.87. Because percentages are always out of 100, they are generally simpler to use than fractions when comparing quantities. Common uses of percentages include commissions, deductions, taxes, discounts, markups, profits, losses, and interest rates. [2]
Percentage Change
Percentage change is the measure of change in a quantity (increase or decrease) expressed as a percent.
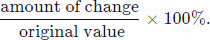
Example 1 – Decrease
Imagine a city with 10,000 people at the beginning of a year. Given that the population at the end of that year is 9,500, compute the percentage change of the population.
Answer 1 – Decrease
The population changed by 10000 − 9500 = 500 people. The percent change in the population is
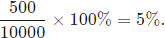
Example 2 – Increase
The price of a sweatshirt changed from $20 to $30. Find the percentage change in the price of the sweatshirt.
Answer 2 – Increase
The change in price of the sweatshirt is $10, and the original price of the sweatshirt was $20. Therefore, the percentage change in the price of the sweatshirt is
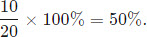
| Take Away |
|---|
|
Do not confuse the percentage decrease, or increase, with the amount of decrease, or increase, or the percent difference. We will use the distributive property to demonstrate.
Ed’s new shirt is on sale for 15% off the original price of $36.00. How much will Ed pay for the shirt not accounting for sales tax? Cost = $36 – ($36 * 0.15) = $36(1 – 0.15) = $36*0.85 = $30.60 Note that we are looking for the final price after 15% off. If the question was how much money did Ed save, we would calculate $36 * 0.15 = $5.40. Looking at our use of the distributive property, the question could have been by how much was the price reduced, and the answer would be 85% (i.e., (1 – 0.15)*100). Patrick wants to by his girlfriend a diamond tennis bracelet. The wholesale price of the bracelet is $320. The markup on diamond jewelry is 420%. How much will Patrick pay for the bracelet not accounting for sales tax? Cost = $320 + ($320 * 4.2) = $320(1 + 4.2) = $320*5.2 = $1644.00 Note that we are looking for the final price after 420% markup. If the question was how much money did Ed pay above the wholesale price, we would calculate $320 * 4.2 = $1344.00. Looking at our use of the distributive property, the question could have been by how much was the price increase, and the answer would be 520% (i.e., (1 + 4.2)*100). Word problems in mathematics often pose a challenge because they require that students read and comprehend the text of the problem, identify the question that needs to be answered, and finally create and solve a numerical equation. |
Percentage Change Calculator (Opens in a new tab/window)
Percentage Difference Calculator (Opens in a new tab/window)
Percentage Error
Percent errors indicate how big our errors are when we measure something in an analysis process. Smaller percent errors indicate that we are close to the accepted or original value. For example, a 1% error indicates that we got very close to the accepted value, while 48% means that we were quite a long way off from the true value. Measurement errors are often unavoidable due to certain reasons like hands can shake, material can be imprecise, or our instruments just might not have the capability to estimate exactly. Percent error formula will let us know how seriously these inevitable errors influenced our results.
Percent error is the difference between estimated value and the actual value in comparison to the actual value and is expressed as a percentage. In other words, the percent error is the relative error multiplied by 100. [7]
The formula for percent error is:
PE = ( |Estimated value – Actual value| / Actual value ) x 100
or
T = True or Actual value
E = Estimated value
Percent Error Calculator (Opens in a new tab/window)
Tips, Taxes, and Discounts
- Discount = Multiply the regular price by the rate of discount
- Selling price = original price – discount
- Tax: To find tax, multiply the tax rate to the taxable amount (income, property value, etc.)
- Tip: To find tip, multiply the rate to the selling price. [4]
Discount, Tax and Tip – Example 1
With a 20% discount, Ella was able to save $40 on a dress. What was the original price of the dress?
20% of x = 40 => 0.20x = 40
Solving for x
x = (40 × 100)/20 = 200
Discount, Tax and Tip – Example 2:
Sophia purchased a sofa for $340.00. The sofa is regularly priced at $400.00. What was the percent discount Sophia received on the sofa?
Use this formula: percent = part ÷ base
340 ÷ 400 = 0.85 = 85%
Therefore, the discount is: 100% – 85%=15%
Discount, Tax, and Tip – Example 3:
Ella and her friends went out to eat at a restaurant. If their bill was $60.00 and they gave their server a 15% tip, how much did they pay altogether?
To solve 15% of 60 use this formula: part = (percent ÷ 100) × whole
part = 15/100 × 60
part = (15 × 60)/100
=90/10
=9
The final amount they paid: $60.00 + $9.00 = $69.00
Discount, Tax and Tip – Example 4:
The selling price of a table is $400 and the tax rate is 6%. What is the final price of the table?
Find tax amount: 6% of 400
To solve 6% of 400 use this formula: part = (percent/100) x whole
part = 6/100 × 400
part = (6 × 400)/100
part = 2400/100
part = 24
The final price of the table is: $400 + $24 = $424
Commissions
This is a very basic calculation revolving around percentages. Just take the sale price, multiply it by the commission percentage, and divide it by 100. An example calculation: a blue widget is sold for $70. The salesperson works on a commission — they get 14% out of every transaction, which amounts to $9.80.
So the formula is:
commission amount = sale price × (commission percentage/100).
So now you know how to calculate commission. Now that you have this figure, there’s a problem with who will cover this cost — usually, it’s the selling party (whoever hired the salesperson to do the job). To calculate their revenue, we need to calculate the percentage decrease:
real revenue = sale price - (sale price × commission percentage/100). In our example, it’s
$70 - ($70 × 14/100) = $70 - $9.80 = $60.20.
It’s not very common, but sometimes it’s the buyer who pays for the salesperson’s remuneration. In those cases, we need the percentage increase formula:
price with commission = base price + (base price × commission percentage/100).
In our example, it’s $70 + ($70 × 14/100) = $70 + $9.80 = $79.80. [3]
Slides
Please wait for the Google Slides to load.
Download the PDF version of the slides.
References
[1] “What Are Percentages and How To Calculate Percentages?” 2021. Full Potential Learning Academy. June 3. https://www.fullpotentialtutor.com/what-are-percentages-and-how-to-calculate-percentages/.
[2] “Applications of Percentages.” 2023. Brilliant Math & Science Wiki. Accessed November 9. https://brilliant.org/wiki/applications-of-percentages/.
[3] Pál, Tibor, and Mateusz Mucha. 2023. “Commission Calculator.” Omni Calculator. Omni Calculator. August 3. https://www.omnicalculator.com/finance/commission.
[4] Effortless Math Team. 1969. “How to Find Discount, Tax, and Tip? (+FREE Worksheet!).” Effortless Math: We Help Students Learn to LOVE Mathematics. Effortless Math Team. December 30. https://www.effortlessmath.com/math-topics/discount-tax-and-tip/.
[5] “Percent Difference – Definition, Examples, How to Calculate?” 2024. Cuemath. Accessed January 13. https://www.cuemath.com/commercial-math/percent-difference/.
[6] “7.3: Solving Basic Percent Problems.” 2020. Mathematics LibreTexts. LibreTexts. August 15. https://math.libretexts.org/Bookshelves/PreAlgebra/Prealgebra_(Arnold)/07%3A_Percent/7.03%3A_Solving_Basic_Percent_Problems.
[7] “Percent Error – Definition, Formula, and Solved Examples.” 2020. BYJUS. BYJU’S. https://byjus.com/maths/percent-error/.
Additional Reading
Díez, Álvaro, and Dominik Czernia. 2023. “Percentage Difference Calculator.” Omni Calculator. Omni Calculator. November 6. https://www.omnicalculator.com/math/percentage-difference#what-is-percentage-difference.
“Formula for Percentage.” 2023. Basic. Accessed November 9. https://www.basic-mathematics.com/formula-for-percentage.html.
“Fraction to Percent (Converting Fractional Numbers to Percentage).” 2023. BYJUS. BYJU’S. October 3. https://byjus.com/maths/fraction-to-percent/.
The term percent is a ratio or a number that is expressed as a fraction of 100. It is denoted using the percentage sign %. To understand the concept of how the percent represents the fraction of 100, here is an example. 35% can be written in fraction as 35/100. In class, 50% of the students were male, which means out of every 100 students, 50 were male.
“How To Calculate Percentage Decrease (With Examples)”. 2023. Indeed. Accessed November 8. https://www.indeed.com/career-advice/career-development/how-to-calculate-percentage-decrease.
“How To Calculate Percentage of a Number (With Examples)”. 2023. Indeed. Accessed November 8. https://www.indeed.com/career-advice/career-development/how-to-calculate-percentage-of-a-number.
“How To Calculate Percentages (With Formula and Examples)”. 2023. Indeed. Accessed November 8. https://www.indeed.com/career-advice/career-development/how-to-calculate-percentages.
“Percent Difference – Explanation & Examples.” 2023. The Story of Mathematics. February 24. https://www.storyofmathematics.com/percent-difference/.
“Percent Proportion – How to Find Percent Proportion?, Meaning, Formula, Examples.” 2023. CUEMATH. Accessed November 23. https://www.cuemath.com/commercial-math/percent-proportion/.
“Percentage: Formula, How to Calculate, Examples and FAQs.” 2023. GeeksforGeeks. GeeksforGeeks. August 16. https://www.geeksforgeeks.org/percentage/.
“Percentages – Aptitude Questions and Answers.” 2023. GeeksforGeeks. GeeksforGeeks. March 7. https://www.geeksforgeeks.org/percentage-aptitude-questions/.
“What Is the Percentage Increase Formula? (With Examples)”. 2023. Accessed November 9. https://www.indeed.com/career-advice/career-development/percent-increase-formula.
Videos
An introduction to the concept of relative difference, or comparing two values using a percentage. All we need to do is write the fraction DIFFERENCE/REFERENCE and then convert that into a percentage. The “difference” is the difference between the two values we are comparing. The reference value could be one of the two values, if it is clear that we are comparing one item to the other. For example, if the question is how many percent taller is the oak tree than a birch tree, then the comparison is TO the birch tree so its height is the reference value. If it’s not clear which of the two is the “reference item”, then you can use the average of the two values as the reference value. However, this last situation is not deal with in the video.
The featured image on this page is from the Full Potential Learning Academy website.
