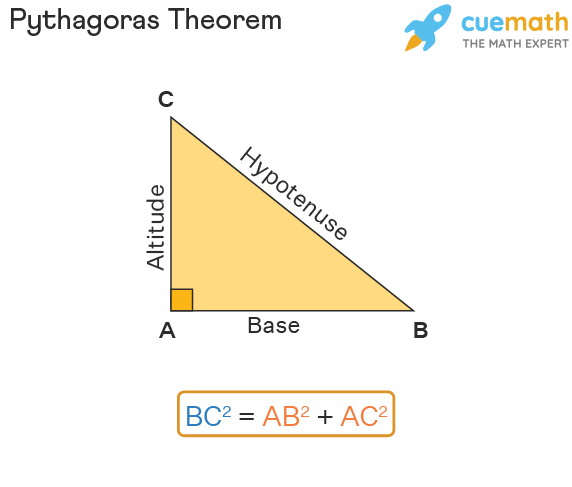
The Pythagoras theorem states that if a triangle is a right-angled triangle, then the square of the hypotenuse is equal to the sum of the squares of the other two sides. Observe the following triangle ABC, in which we have BC2 = AB2 + AC2. Here, AB is the base, AC is the altitude (height), and BC is the hypotenuse. It is to be noted that the hypotenuse is the longest side of a right-angled triangle. [1]
Pythagoras Theorem
The Pythagoras theorem equation is expressed as, c2 = a2 + b2, where ‘c’ = hypotenuse of the right triangle and ‘a’ and ‘b’ are the other two legs. Hence, any triangle with one angle equal to 90 degrees produces a Pythagoras triangle and the Pythagoras equation can be applied in the triangle. [1]
Pythagorean Triples
Pythagorean triples are any three positive integers that completely satisfy the Pythagorean theorem. The theorem states that in any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two legs of the right triangle. These three sides of the right triangle form the Pythagorean triples. [2]
“The Babylonians had also discovered that, for any odd number n, the lengths
would form the three sides of a right triangle. Using these formulas, they were able to create an unlimited number of right triangles whose sides were whole numbers.” [3]
History of Pythagoras Theorem
Pythagoras theorem was introduced by the Greek Mathematician Pythagoras of Samos. He was an ancient Greek philosopher who formed a group of mathematicians who worked religiously on numbers and lived like monks. Although Pythagoras introduced the theorem, there is evidence that proves that it existed in other civilizations too, 1000 years before Pythagoras was born. The oldest known evidence is seen between the 20th to the 16th century B.C in the Old Babylonian Period. [1]
References
[1] “Pythagoras Theorem – Formula, Proof, Examples.” 2023. CUEMATH. Accessed November 23. https://www.cuemath.com/geometry/pythagoras-theorem/.
[2] “Quiz About Pythagorean Triples.” 2026. CUEMATH. Accessed January 8. https://www.cuemath.com/geometry/pythagorean-triples/.
[3] Bradley, Michael J. The Birth of Mathematics: Ancient Times to 1300 (Pioneers in Mathematics). New York: Chelsea House, 2006.
Additional Reading
Baker, Steve. “In Your Opinion, What Is the Best Proof of the Pythagorean Theorem?” 2023. Quora. Accessed November 23. https://qr.ae/pKMhnN.
Bogomolny, Alexander. 2025. “Pythagorean Theorem.” Pythagorean Theorem and Its Many Proofs. Accessed August 4. https://www.cut-the-knot.org/pythagoras/.
Professor R. Smullyan in his book 5000 B.C. and Other Philosophical Fantasies tells of an experiment he ran in one of his geometry classes. He drew a right triangle on the board with squares on the hypotenuse and legs and observed the fact the the square on the hypotenuse had a larger area than either of the other two squares. Then he asked, “Suppose these three squares were made of beaten gold, and you were offered either the one large square or the two small squares. Which would you choose?” Interestingly enough, about half the class opted for the one large square and half for the two small squares. Both groups were equally amazed when told that it would make no difference.
McNulty, Keith. 2024. “How Two Teenagers Found a New Proof of the Pythagorean Theorem.” Medium. Medium. October 11. https://medium.com/@keith-mcnulty/how-two-teenagers-found-a-new-proof-of-the-pythagorean-theorem-eebf7b6c061c.
Recently, two teenage girls — Calcea Johnson and Ne’Kiya Jackson — gave a presentation to the American Mathematical Society where they demonstrated a new proof of the Pythagorean Theorem. Their proof has caused quite a stir.
“Pythagoras Theorem – Formula, Proof, Examples, Applications.” 2023. BYJUS. BYJU’S. June 13. https://byjus.com/maths/pythagoras-theorem/.
Videos
 Medium Member Only
Medium Member Only
The featured image on this page is from the YouTube video Proving the Pythagorean Theorem.
