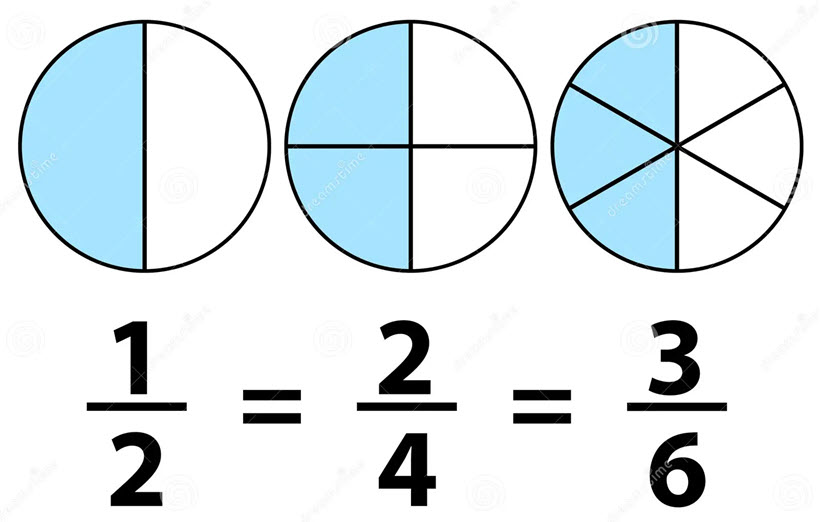Fractions
A fraction is a way to represent a part of a whole. It consists of two numbers:
- Numerator: The top number, which indicates how many parts you have.
- Denominator: The bottom number, which shows how many equal parts the whole is divided into.
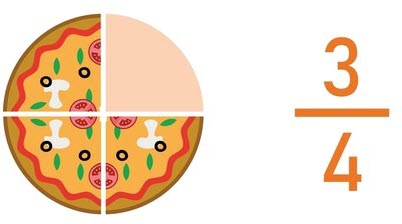
For example, in the fraction 3/4:
- The numerator (3) indicates that you have 3 parts.
- The denominator (4) indicates that the whole is divided into 4 equal parts.
Fractions can represent values less than 1 (proper fractions), equal to 1 (unit fractions), or greater than 1 (improper fractions). Fractions are fundamental in mathematics for describing ratios, divisions, and proportions.
NOTE
In essence, “equivalent fractions” and “proportions” are the same concept, as both refer to two ratios or fractions that represent the same value, even if they look different; a proportion is simply a statement that two ratios are equal, which means they are considered equivalent fractions.
Equivalent Fractions
The meaning of ‘equivalent’ generally refers to two numbers, expressions, or quantities with the same value. Equivalence is similar but not the same as equality.
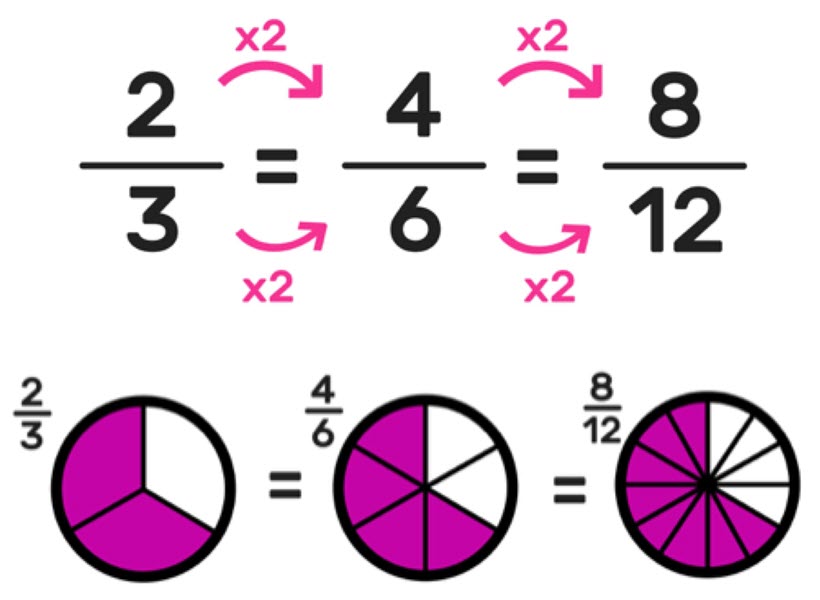
Equivalent fractions are different fractions that represent the same value or proportion of a whole. They may have different numerators and denominators, but when reduced, they simplify to the same ratio.
Equivalent fractions state that two or more fractions are said to be equal if both result in the same fraction after simplification. Let us say a/b and c/d are two fractions. After the simplification of these fractions, both result in equivalent fractions, say e/f, and then they are equal to each other.
For example, the equivalent fraction of 1/3 is 5/15, because if we simplify 5/15, the resulting fraction is the same.

Equivalent fractions are useful in adding, subtracting, and comparing fractions, as they allow for common denominators and a clearer understanding of proportional relationships [1].
The biggest question is why they have equal values despite having different numbers. The answer is that, as the numerator and denominator are not co-prime numbers [2], they have a common multiple, which, on division, gives precisely the same value.
NOTE
When you multiply or divide the numerator and denominator by the same number (multiplying by one, e.g., 2/2, 5/5, 9/9), the fraction keeps its value because you are using the same proportional value for the numerator and the denominator. For example, 2/3 * 2/2 = 4/6. So, 2/3 is equivalent to 4/6 because the proportional amount – in this case, 2 – is the same for both the numerator and denominator.
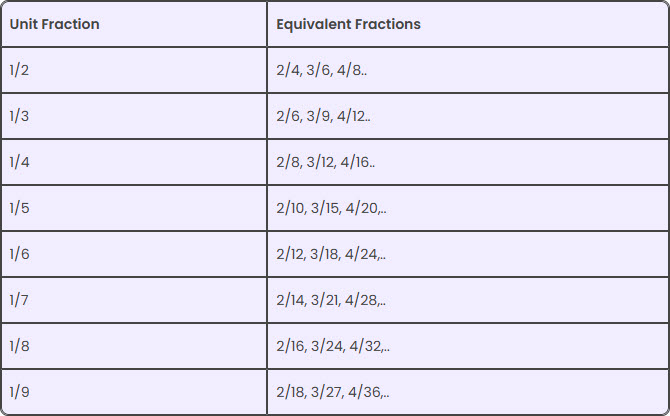
Method to Determine If Fractions Are Equivalent
Given two fractions 1/2 and 3/6, cross multiply both the fractions to get:
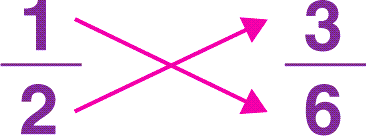
1 x 6 = 6
2 x 3 = 6
Since, both the values are equal, therefore, 1/2 and 3/6 are equivalent fractions.
Tips
- You can make equivalent fractions by multiplying or dividing both top and bottom by the same amount.
- You only multiply or divide, never add or subtract, to get an equivalent fraction.
- Only divide when the top and bottom stay as whole numbers.
References
“Equivalent Fractions – Definition, How to Find Equivalent Fractions, Examples.” 2022. BYJUS. BYJU’S. August 24. https://byjus.com/maths/equivalent-fractions/.
“Equivalent Fractions.” 2025. Math Is Fun. Accessed January 19. https://www.mathsisfun.com/equivalent_fractions.html.
Persico, Anthony. 2024. “Equivalent Fractions Explained-Definitions, Examples, Worksheets.” Mashup Math. Mashup Math. October 4. https://www.mashupmath.com/blog/equivalent-fractions-explained.
“What Are Equivalent Fractions? (Comparison, Models, Examples) – BYJUS.” 2022. BYJU’S. September 19. https://byjus.com/us/math/equivalent-fractions-and-their-comparison/.
“What is Equivalent? Definition, Applications, Example, Facts.” 2024. SplashLearn. https://www.splashlearn.com/math-vocabulary/number-sense/equivalent.
Notes
[1] A proportional relationship is a relationship between two variables that change at a constant rate. This means that the ratio between the two variables is always the same.
- Constant of proportionality: The constant ratio between the two variables. It’s represented by the letter 𝑘 (constant of proportionality) in the equation 𝑦=𝑘𝑥.
- Identifying proportional relationships: To determine if a relationship is proportional, check if the ratio between the two variables is always the same.
- Real-world example: If you’re baking and you need 2 cups of flour for every 1 cup of sugar, the ratio is 2:1. This ratio stays the same no matter how much flour and sugar you use.
[2] Co-prime numbers are two or more numbers with no common factors other than 1. The greatest common factor (GCF) of co-prime numbers is always 1.