K-12 – Division – Mathematical Mysteries

Division is the inverse of the multiplication operation. It is defined as the act of forming equal groups. While dividing numbers, we break down a larger number into smaller numbers such that the multiplication of those smaller numbers will be equal to the larger number taken. For example, 4 ÷ 2 = 2. This can be written as a multiplication fact as 2 × 2 = 4. [1]

Contents

Isn’t division the process of repetitive subtraction? In some cases the answer is yes! For example 32 ÷ 8 is the same as 32 – 8 – 8 – 8 – 8. In the example below, we also see that division uses subtraction and multiplication to show that we can “divide” 906 into 6 equal parts of 151.

Even when we divide a natural number by a fraction (i.e., a smaller number from, a larger number), we can understand that one can be divided into 5 pieces.

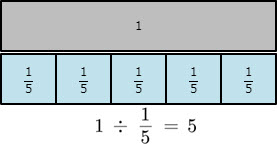
When I divide, shouldn’t the number become smaller, e.g., 20 ÷ 4 = 5 where 5 < 20, and not 1 ÷ ⅕ = 5 where 5 > 1?

Someone may then ask: How do I repetitively subtract 36 from 18 (18 ÷ 36 = ½), or repetitively subtract 8 from ½ (½ ÷ 8 = 1/16)? (See the Dividing Natural Numbers, Fractions and Improper Fractions slides below.)

When a student encounters these types of problems, their understanding of what division is may be challenged, and they find learning these new division concepts harder to grasp. Therefore, when we speak about division, we should use one of the following statements to really convey the concept.

How many times does the divisor fit inside the dividend, e.g., 906 ÷ 6 = 151.
How much of the divisor fits into the dividend, e.g., 1 ÷ ⅕ = 5.

Dividing Natural Numbers, Fractions and Improper Fractions

Please wait for the Google Slides to load.
Download the PDF version of the slides.

Remember when you get stuck, think about the problem and draw a picture.

How to Get Started with Long Division

We will learn how to solve double digit division using the following example.

Part 1

Take the first digits of the dividend: in this case 57. But as 57 is smaller than 73, you have to take one more digit: 573.
To divide 573 by 73, we take the first two digits of the dividend 57, and divide them by the first digit of the divisor:

58 ÷ 7 = 8
Write the 8 in the quotient and multiply it by the divisor:

8 x 73 = 584

But 584 is bigger than 573; therefore, 8 “does not fit”. You have to choose the preceding number and multiply again:

7 x 73 = 511

511 is smaller than the dividend; therefore 7 “does fit”. We write 511 beneath the digits of the dividend and then divide and subtract.
Drop the next digit of the dividend, which is 8. Now, you have to divide 628 by 73.

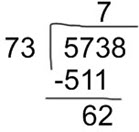
Part 2

Repeat the previous steps.

Divide the first two digits of the dividend by the first digit of the divisor and write it in the space of the quotient:

62 ÷ 7 = 8
Multiply that digit by the divisor:

8 x 73 = 584
584 is less than 628; therefore, we can subtract:

628 – 584 = 44

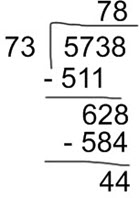
The result of this division is 78 and a remainder of 44.

References

[1] “Division – Meaning, Steps, Algorithm, Examples.” 2024. CUEMATH. Accessed February 4. https://www.cuemath.com/numbers/division/.

Additional Reading

“Dividing Fractions with Whole Numbers – Steps & Examples.” 2024. CUEMATH. Accessed February 13. https://www.cuemath.com/numbers/dividing-fractions-with-whole-numbers/.

“Division of Fractions – Steps, Method, Examples.” 2024. CUEMATH. Accessed February 13. https://www.cuemath.com/numbers/division-of-fractions/.

“Formula for Dividing Fractions – What Is Dividing Fractions Formula?” 2024. CUEMATH. Accessed February 13. https://www.cuemath.com/dividing-fractions-formula/.

“IXL: Learn Division.” 2024. IXL Learning. Accessed September 28. https://www.ixl.com/math/division.

Here is a list of all of the skills that cover division! These skills are organized by grade, and you can move your mouse over any skill name to preview the skill. To start practicing, just click on any link. IXL will track your score, and the questions will automatically increase in difficulty as you improve!

Videos

Bob the Counting Sheep and Jo Boaler divide one by two-thirds.

Google Slides References

“7 Strategies to Teach Conceptual Understanding in Math.” 2024. Blog | Carnegie Learning. Accessed August 10. https://www.carnegielearning.com/blog/strategies-to-teach-math-conceptual-understanding/.

Boaler, Jo, Mathematical Mindsets: Unleashing Students’ Potential through Creative Math, Inspiring Messages and Innovative Teaching, Second Edition. (Hoboken, NJ: Jossey-Bass, 2022).

Crandell, Cassie. 2021. “How to Teach Dividing Fractions With Models: FREE Practice.” Math Geek Mama. February 18. https://mathgeekmama.com/how-to-teach-dividing-fractions/.

“Dividing Fractions with Whole Numbers – Steps & Examples.” 2024. Cuemath. Accessed August 16. https://www.cuemath.com/numbers/dividing-fractions-with-whole-numbers/.

“Division Involving Fractions.”2024. Fraction Bars Workshop – Division. Accessed August 16. https://fractionbars.com/Grades5to8/FracBarOperations/Division.html.

FractionBars. “Division Step 1 – Model Dividing Fractions by Fractions (Video #19).” 2024. YouTube. YouTube. Accessed August 14. https://www.youtube.com/watch?v=tBxPYosbyWw&t=10s.

FractionBars. “Division Step 2 – Dividing by Fractions and Whole Numbers (Video #20).” 2024. YouTube. YouTube. Accessed August 14. https://www.youtube.com/watch?v=ZM9Ym-HCbN8&t=57s.

FractionBars. “Division Step 3 – Whole Number Quotients (Video #21).” 2024. YouTube. YouTube. Accessed August 14. https://www.youtube.com/watch?v=eGGhtCxU784&t=13s.

JB. “Conceptual Understanding of Division with Fractions (Using Models).” 2024. YouTube. YouTube. Accessed August 14. https://www.youtube.com/watch?v=k7FoK55xWl4&t=1s.

Smith, Emily, and Abram Bafana Morodi. 2022. “Conceptual & Procedural Math: What’s the Difference?” Well Trained Mind. https://welltrainedmind.com/a/conceptural-procedural-math-whats-the-difference/.

“Teaching Division for Conceptual Understanding.” 2022. Room to Discover. May 4. https://roomtodiscover.com/teaching-division/.

“Teaching Fraction Division: A Visual and Conceptual Approach.” 2022. Room to Discover. May 24. https://roomtodiscover.com/teaching-fraction-division-visual-conceptual/.

“Why Do We ‘invert’ the Divisor in Division of Fractions.” 2019. Mathematics for Teaching. https://math4teaching.com/division-of-fractions/.

The featured image on this page is from the ShowMe website.