K-12 – Decimals – Mathematical Mysteries

Contents

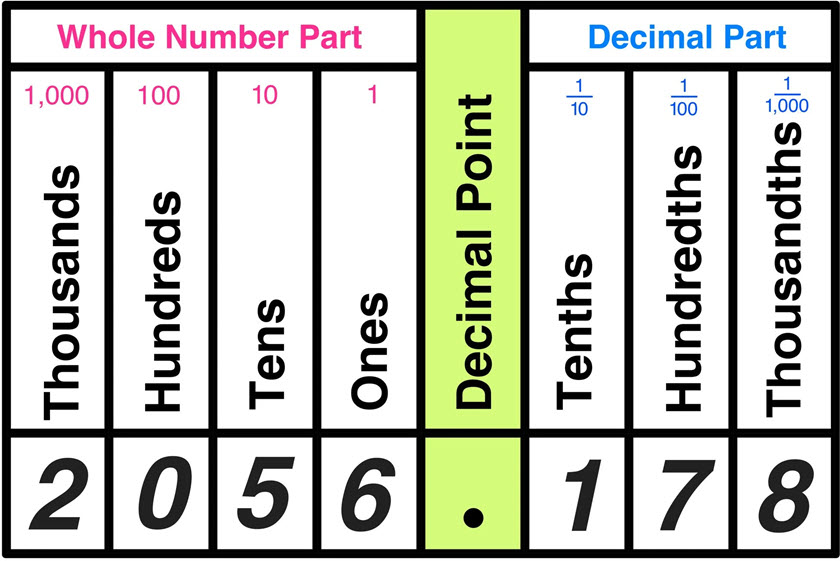
Decimals

A decimal (or decimal number) in mathematics is a number expressed in the base-10 (denary) positional numeral system, using digits 0–9 and a decimal point (.) to separate the integer part from the fractional part. Decimals enable precise fractional arithmetic in base-10, common in computation and measurement (e.g., 0.01 m = 1 cm).

Structure

Integer part: Digits to the left of the decimal point
(e.g., 123 in 123.456 and means 100 + 20 + 3).
Fractional part: Digits to the right, representing fractions of 1
(e.g., 456 means $\frac{4}{10} + \frac{5}{100} + \frac{6}{1000}$ ).
Pure integer: No decimal point or fractional digits (e.g., 5 = 5.0).
Terminating decimal: Finite fractional digits (e.g., 0.75 = $\frac{3}{4}$ ).
Repeating decimal: Infinite repeating block (e.g., 0.333… = $\frac{1}{3}$ ; notated as 0.3)

Distinctions

vs. Fraction: Decimals are decimal expansions of rationals (all terminating/repeating); irrationals (e.g., π≈3.14159…, non-repeating) have infinite non-repeating decimals.
vs. Binary/Hex: Base-10 specific; binary uses base-2 (e.g., 0.1₂ = 0.5₁₀).
Finite vs. Infinite: All reals have decimal representations, but rationals terminate or repeat.

Important Observation

Adding zeros to the end of the fractional part of a decimal number does not change its value. Similarly, deleting trailing zeros from the end of a decimal number does not change its value.

$7.2500=7\frac{2500}{10000}=7\frac{25}{100}=7.25$

Addition & Subtraction

Addition

To add decimals, line up the decimal points vertically, add placeholder zeros if needed to align place values, then add from right to left like regular numbers, bringing the decimal point straight down into your answer. This key method ensures you add tenths to tenths, hundredths to hundredths, and so on, making the process straightforward and accurate.

This method works for adding decimals to whole numbers as any whole number has an unwritten decimal point after it (e.g., 7 is 7.0).

Subtraction

To subtract, follow the same method as in addition, i.e., line up the decimal points, then subtract.

Common Mistake

Forgetting to line up the decimal points: This is the most common error; lining them up correctly prevents place value mistakes.

Examples

See the following web pages for examples of adding and subtracting decimals.

Multiplication

To multiply decimals, treat them as whole numbers first, then count the total number of digits after the decimal point in the original numbers and place the decimal point that many places from the right in your answer, adding zeros as placeholders if needed. For example, to multiply 0.3 x 0.4, multiply 3 x 4 to get 12, then count the one decimal place in 0.3 and one in 0.4 (total of two), so your answer is 0.12.

TBS

$0.3\times 0.4 =\,\,\frac{3}{10}\times \frac{4}{10}\,\,=\,\,\frac{12}{100}\,\,=\,\,0.12$

Step-by-Step Guide

Ignore decimals & multiply: Multiply the numbers as if they were whole numbers (e.g., for 1.4 x 0.23, do 14 x 23 = 322).
Count decimal places: Count how many digits are to the right of the decimal point in each original number (i.e., 1 decimal place for 1.4 and 2 decimal places for 0.23).
Add them up: Sum the counts from Step 2 to find the total number of decimal places for your answer (i.e., 1 decimal place for 1.4 and 2 decimal places for 0.23 for a total of 3 decimal places).
Place the decimal: Starting from the right of your whole-number product (i.e., 322. ), move the decimal point to the left the total number of places you counted in Step 3 (i.e., 0.322).

Examples

See the following web pages for examples of multiplying decimals.

Division

Decimal division involves splitting numbers with decimals into equal parts, primarily using long division but requiring special handling of the decimal point: for a decimal divisor, move its decimal to make it a whole number and move the dividend’s decimal the same amount; for a whole number divisor, place the decimal point in the answer directly above its position in the dividend, then follow standard divide, multiply, subtract, bring down, repeat steps.

Dividing by a Whole Number

Example: 12.5 ÷ 2

Set up: Place the decimal point in the quotient (answer) directly above the decimal point in the dividend (12.5).
Divide: Solve as you would with whole numbers (How many times does 2 go into 12? 6).
Multiply: 6×2=12.
Subtract: 12−12=0.
Bring Down: Bring down the next digit (5).
Repeat: How many times does 2 go into 5? 2 times (2×2=4). Subtract (5-4=1). Add a zero to the dividend (12.50) and bring it down (10). 2 goes into 10 five times.
Answer: 12.5 ÷ 2 = 6.25.

TBS

$12.5 \div \,\,2 =\,\,12\frac{5}{10}\,\,\div \,\,2 =\,\,\frac{125}{10}\,\,\div \,\,2$

Using Keep, Change, Flip to solve the expression, and changing the improper fraction into a decimal.

$\frac{125}{10}\,\,\times \,\,\frac{1}{2}\,\,=\,\,\frac{125}{20}\,\,=\,\,\frac{25}{4}\,\,=\,\,6.25$

Dividing by a Decimal

Example: 12.5 ÷ 0.5

Adjust the Divisor: Move the decimal point in the divisor (0.5) to the right until it becomes a whole number (5). You moved it one place.
Adjust the Dividend: Move the decimal point in the dividend (12.5) the same number of places to the right (one place), making it 125.
Set up: Now you’re dividing 125 by 5. Place the decimal in the answer above the new decimal in the dividend (which is at the end of 125).
Divide: Solve 125 ÷ 5. 5 goes into 12 two times, remainder 2. Bring down the 5 to make 25. 5 goes into 25 five times.
Answer: 12.5 ÷ 0.5 = 25.

TBS

$12.5 \div \,\,0.5 =\,\,12\frac{5}{10}\,\,\div \,\,\frac{5}{10}\,\,=\,\,\frac{125}{10}\,\,\div \,\,\frac{5}{10}$

Using Keep, Change, Flip to solve the expression, and changing the improper fraction into a decimal or leave as a whole number as needed.

$\frac{125}{10}\,\,\times \,\,\frac{10}{5}\,\,=\,\,\frac{125}{5}\,\,=\,\,25$

Converting Decimal to a Fraction

TBS

Scientific Notation

Scientific Notation (also called standard form or exponential notation) is a compact way to write very large or very small numbers.

It always follows this exact format:

a × 10^b

Where:

a is a decimal number ≥ 1 and < 10 (written with 1 digit before the decimal point)
b is an integer (positive, negative, or zero)

Normal Number	Scientific Notation	Meaning
5,600	5.6×10³	5.6 × 1,000 = 5,600
720,000,000	7.2 × 10⁸	7.2 × 100,000,000
0.00034	3.4×10^-4	3.4 ÷ 10,000
0.000000092	9.2×10^-8	9.2 ÷ 100,000,000
6,022,000,000,000,000,000,000	6.022 × 10²¹	Avogadro’s number (~particles/mol)
0.00000000000000000016	1.6 × 10^-19	Charge of one electron (coulombs)

Quick Examples

Exponent	Value	Name
10⁰	1
10¹	10
10³	1,000	kilo
10⁶	1,000,000	mega
10⁹	1,000,000,000	giga
10¹²	1,000,000,000,000	tera
10^-3	0.001	milli
10^-6	0.000001	micro
10^-9	0.000000001	nano
10^-12	0.000000000001	pico

Common Patterns to Recognize

Keep, Change, Flip

“Keep, Change, Flip” (KCF) is a mnemonic for dividing fractions: Keep the first fraction, Change the division sign to multiplication, and Flip (find the reciprocal of) the second fraction, then multiply as usual. This method simplifies dividing by a fraction into multiplying by its reciprocal, making the problem solvable by standard multiplication.

Example to solve $two-sevenths divided by three-fifths$

Keep: $two-sevenths$
Change: ÷ to ×
Flip: $five-thirds$
Multiply: $two-sevenths cross five-thirds equals 10 over 21 end-fraction$

References

TBS

Additional Reading

“Decimal.” Wikipedia, December 29, 2025. https://en.wikipedia.org/wiki/Decimal.

Persico, Anthony. “Where Is the Hundredths Place Value in Math? — Mashup Math.” Mashup Math, December 11, 2022. https://www.mashupmath.com/blog/hundredths-place-value-hundredths-chart.

The featured image on this page is from the mashupmath website.