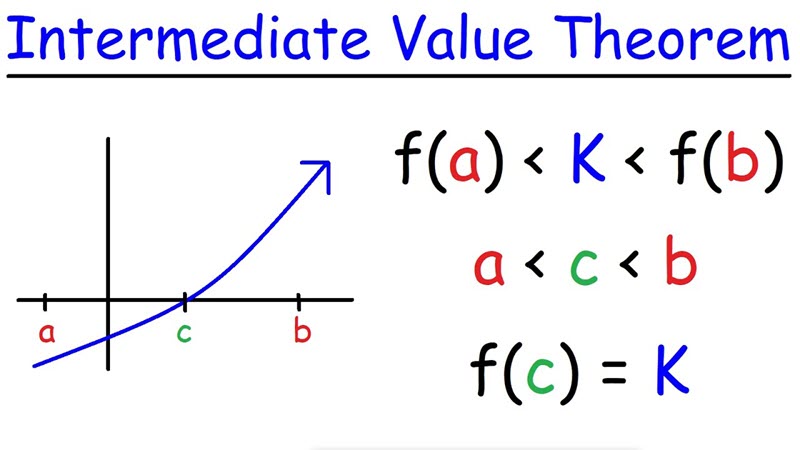
Definition
The intermediate value theorem states that if a continuous function attains two values, it must also attain all values in between these two values. Intuitively, a continuous function is a function whose graph can be drawn “without lifting pencil from paper.” For instance, if f(x) is a continuous function that connects the points [0,0] and [5,20], then there must be some xa between 0 and 5 where y=1, also some xb where y=19, another xc where y=19/5, etc. For this function there is an x∈[0,5] for any y value between 0 and 20. [1]

– Brilliant

The statement of intermediate value theorem seems to be complicated. But it can be understood in simpler words. Let us consider the below diagram, there is a continuous function f with endpoints a and b, then the height of the point a and b would be f(a) and f(b).
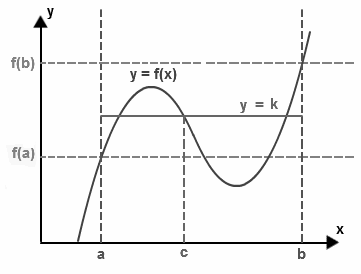
If we pick a height k between these heights f(a) and f(b), then according to this theorem, this line must intersect the function f at some point (say c), and this point must lie between a and b.
An intermediate value theorem, if c = 0, then it is referred to as Bolzano’s theorem. [2]
The intermediate value theorem offers one way to find roots of a continuous function. An informal definition of continuous is that a function is continuous over a certain interval if it has no breaks, jumps, asymptotes, or holes in that interval. Polynomial functions are continuous for all real numbers x. Rational functions are often not continuous over the set of real numbers because of asymptotes or holes in the graph, but for intervals without holes, rational functions are continuous. [3]
Who
This intermediate value theorem has many implications in solving problems in Mathematics, Statistics, Physics, Chemistry and other fields of study. It is applicable whenever there is a continuously varying scalar quantity [e.g., pressure, temperature, elevation, and carbon dioxide gas concentration] with endpoints sharing the same value for a variable. [2]
What
The intermediate value theorem has many applications. Mathematically, it is used in many areas. This theorem is utilized to prove that there exists a point below or above a given particular line. It is also used to analyze the continuity of a function that is continuous or not. [2]
Why
A simple real world example of how the theory works: You measure the weight of your new puppy and she is 15 lbs. Ten days later she weights 18 lbs. That gives you two points on your closed interval:
- f(a) = f(0) = 15 lbs
- f(b) = f(10) = 18 lbs
Let’s say you wanted to pinpoint the moment when your puppy weighed c = 16.5 lbs. The IVT tells you that this point c must exist. It might take you a while to pinpoint that exact time, but you know your time isn’t going to be wasted. This simple example can be extended to any problem in science that involves pinpointing a specific time, weight, or other metric. For example, carbon dating an object typically takes several days to process, so it’s nice to know from the outset that a solution is possible. Invoking the IVT before you start any complicated technical process saves wasting time and resources on hunting down solutions that may or may not exist. [4]
See Theoretical Knowledge Vs Practical Application.
How
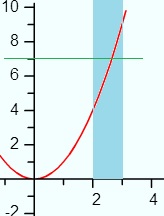
Example: For the function f(x) = x2, show that there is a number m between 2 and 3 such that f(m) = 7.
Step 1: Draw a graph to help you visualize the problem.
– Statistics How To
Step 2: Check for continuity. If the function isn’t continuous, you can’t use the intermediate value theorem. This function is a polynomial function, so we can use the theorem: all polynomials are continuous.
Step 3: Evaluate the function at the lower and upper values given. For this example, you’re given x = 2 and x = 3, so:
- f(2) = 4
- f(3) = 9
7 is between 4 and 9, so there must be some number m between 2 and 3 such that f(c) = 7. [4]
Many of the References and Additional Reading websites and Videos will assist you with understanding and applying the Intermediate Value Theorem.
As some professors say: “It is intuitively obvious to even the most casual observer.“
References
[1] “Intermediate Value Theorem | Brilliant Math & Science Wiki”. 2023. Brilliant.Org. https://brilliant.org/wiki/intermediate-value-theorem/.
[2] “Intermediate Value Theorem (Statement, Proof & Example)”. 2023. BYJUS. https://byjus.com/maths/intermediate-value-theorem/.
[3] “2.6.4: Intermediate Value Theorem”. 2021. K12 LibreTexts. https://k12.libretexts.org/Bookshelves/Mathematics/Analysis/02%3A_Polynomial_and_Rational_Functions/2.06%3A_Finding_Zeros_of_Polynomials/2.6.04%3A_Intermediate_Value_Theorem.
[4] “Intermediate Value Theorem: Definition, Examples”. 2023. Statistics How To. https://www.statisticshowto.com/calculus-problem-solving/intermediate-value-theorem/.
Additional Reading
“1.6: Continuity And The Intermediate Value Theorem”. 2018. Mathematics LibreTexts. https://math.libretexts.org/Courses/Mount_Royal_University/MATH_1200%3A_Calculus_for_Scientists_I/1%3A_Limit__and_Continuity_of_Functions/1.6%3A_Continuity_and_the_Intermediate_Value_Theorem.
“3.2: Intermediate Value Theorem”. 2019. Mathematics LibreTexts. https://math.libretexts.org/Bookshelves/Geometry/Euclidean_Plane_and_its_Relatives_(Petrunin)/03%3A_Half-Planes/3.02%3A_Intermediate_Value_Theorem.
“3.3: Intermediate Value Theorem, Existence Of Solution”. 2020. K12 LibreTexts. https://k12.libretexts.org/Bookshelves/Mathematics/Calculus/03%3A_Limits_-_Continuity/3.03%3A_Intermediate_Value_Theorem_Existence_of_Solution.
“7.2: Proof Of The Intermediate Value Theorem”. 2018. Mathematics LibreTexts. https://math.libretexts.org/Bookshelves/Analysis/Real_Analysis_(Boman_and_Rogers)/07%3A_Intermediate_and_Extreme_Values/7.02%3A_Proof_of_the_Intermediate_Value_Theorem.
“Intermediate Value Theorem”. 2023. CUEMATH. https://www.cuemath.com/calculus/intermediate-value-theorem/.
“Intermediate Value Theorem”. 2023. Desmos. https://www.desmos.com/calculator/sg1fc6swq3.
“Intermediate Value Theorem”. 2023. Khan Academy. https://www.khanacademy.org/math/ap-calculus-ab/ab-limits-new/ab-1-16/v/intermediate-value-theorem.
“Intermediate Value Theorem Problems”. 2023. math.ucdavis.edu. https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/imvtdirectory/IntermediateValueTheorem.html.
Videos
Introduction to the Intermediate value theorem. If f is a continuous function over [a,b], then it takes on every value between f(a) and f(b) over that interval.
Given that a continuous function f obtains f(-2)=3 and f(1)=6, Sal picks the statement that is guaranteed by the Intermediate value theorem.
Example justifying use of intermediate value theorem (where function is defined with a table).
Example justifying use of intermediate value theorem (where function is defined with an equation).
This calculus video tutorial provides a basic introduction into the intermediate value theorem. It explains how to find the zeros of the function such that c is between a and b on the interval [a, b]. This video contains plenty of examples and practice problems.
This calculus video tutorial explains how to use the intermediate value theorem to find the zeros or roots of a polynomial function and how to find the value of c that satisfies the intermediate value theorem on a continuous interval. This contains plenty of examples and practice problems for you to master the concept. It shows you how to factor trinomials with leading coefficient of 1 and when it’s not 1 in order to find the value of c. It also explains the IVT theorem using graphs.
⭐ I suggest that you read the entire reference. Other references can be read in their entirety but I leave that up to you.
The featured image on this page is from the YouTube video Intermediate Value Theorem by The Organic Chemistry Tutor.