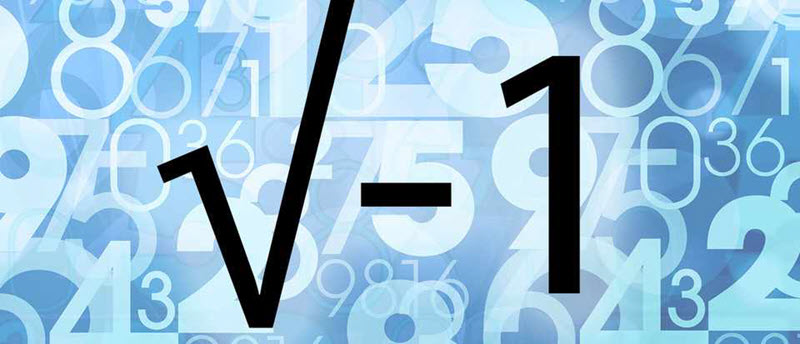History
In 16th century Venice, formulae for solving equations were closely guarded intellectual property. Of particular interest to ballistics and fortifications expert Niccolo Tartaglia were quadratic and cubic equations, which model the behaviour of projectiles in flight amongst other things. These may well ring a bell with you from school maths – quadratic equations have anx2term in them and cubics anx3term. Tartaglia and other mathematicians noticed that some solutions required the square roots of negative numbers, and herein lies a problem. Negative numbers do not have square roots – there is no number that, when multiplied by itself, gives a negative number. This is because negative numbers, when multiplied together, yield a positive result: -2 × -2 = 4 (not -4).
Tartaglia and his rival, Gerolamo Cardano, observed that, if they allowed negative square roots in their calculations, they could still give valid numerical answers (Real numbers, as mathematicians call them). Tartaglia learned this the hard way when he was beaten by one of Cardano’s students in a month-long equation-solving duel in 1530.
Like so many developments in mathematics, all of this was of purely academic interest until the modern electronic age. Complex numbers turn out to be incredibly useful in analysing anything that comes in waves, such as the electromagnetic radiation we use in radios and wifi, audio signals for music and voice communication and alternating current power supplies. Equally, quantum physics reduces all particles to waveforms, meaning that complex numbers are instrumental in understanding this strange world that has allowed us to enjoy modern computers, fibre-optics, GPS, MRI imaging, to name but a few. [1]
Definition
Imaginary numbers are numbers that result in a negative number when squared. They are also defined as the square root of negative numbers. An imaginary number is the product of a non-zero real number and the imaginary unit “i” (which is also known as “iota”), where i = √(-1) or i2 = -1. [2]
Value of i
It turns out that arithmetically, i2=−1. In other words, the value of i is the square root of −1. For now, don’t ask how! As we said earlier, the various different parts of the puzzle that is Complex Numbers will fall into place as you delve deeper into this subject.
At this point, just keep in mind that:
- i is a non-real number (i lies outside the Real set).
- i represents one unit perpendicular to the Real direction.
- yi represents y units perpendicular to the Real direction
- x+iy represents the point (x, y)
- i is the square root of −1 or i2=−1.
When we say that i is a non-real number, we do not mean that i does not exist or is a figment of our imagination. We mean to say that i is non-real in the sense that it does not like in the Real set. However, it is a perfectly valid mathematical entity. i is also known by the name “iota”. [2]
Powers of i
We know that i2 = -1 and using the power rules other powers of I can also be easily calculated. [3]
- i = √-1
- i2 = -1
- i3 = i2×i = -i
- i4 = (i2)2 = (-1)2 = 1
- i5 = i4×i = i
On observing clearly we can see a pattern, there is a cycle of -i, 1, i… after power 2 thus, [3]
- i4n-1= -i
- i4n = 1
- i4n+1= i

Applications of Imaginary Numbers
While imaginary numbers may seem abstract, they have practical applications in various fields. Here are some of these applications: [4]
Electrical Engineering
Imaginary numbers play a crucial role in analyzing and designing electrical circuits. They help represent alternating current (AC) signals and facilitate calculations involving phase shifts and impedance.
Quantum Mechanics
Imaginary numbers are used in quantum mechanics to describe physical phenomena at the atomic and subatomic levels. They enable the formulation of Schrödinger’s equation and provide a mathematical framework for understanding wave-particle duality.
Signal Processing
Imaginary numbers find applications in signal processing, where they help analyze and manipulate complex waveforms. They are particularly useful in Fourier analysis, which decomposes signals into their constituent frequencies.
Euler’s Formula
Euler’s formula establishes a deep connection between trigonometry, complex numbers, and imaginary numbers. It states that e iθ = cos (θ) + i sin (θ), where “e” represents Euler’s number and “θ” is an angle in radians. This formula beautifully relates the exponential function, trigonometric functions, and imaginary numbers.
Computer Graphics
Imaginary numbers are used in computer graphics to represent rotation and scaling.
References
[1] “A Brief History to Imaginary Numbers.” 2024. BBC Science Focus Magazine. Accessed January 11. https://www.sciencefocus.com/science/a-brief-introduction-to-imaginary-numbers.
[2] “Imaginary Numbers – Calculating: Value of i in Math.” 2024. CUEMATH. Accessed January 11. https://www.cuemath.com/numbers/imaginary-numbers/.
[3] “Imaginary Numbers: Definition, Value, Operations, & Examples.” 2023. GeeksforGeeks. GeeksforGeeks. March 25. https://www.geeksforgeeks.org/imaginary-numbers/.
[4] “Imaginary Number: Definition, Properties, and Examples.” 2024. Imaginary Number – Complex Analysis – Properties, and Examples. Accessed January 11. https://www.allmath.com/complex-analysis/imaginary-number.
Additional Reading
“A Visual, Intuitive Guide to Imaginary Numbers.” 2024. BetterExplained. Accessed January 11. https://betterexplained.com/articles/a-visual-intuitive-guide-to-imaginary-numbers/.
“Complex Numbers (Definition, Formulas, Examples).” 2022. BYJUS. BYJU’S. August 25. https://byjus.com/maths/complex-numbers/.
“Complex Number – Definition, Formula, Properties, Examples.” 2024. Cuemath. Accessed January 11. https://www.cuemath.com/numbers/complex-numbers/.
Helmenstine, Anne. 2023. “Imaginary Numbers.” Science Notes and Projects. October 3. https://sciencenotes.org/imaginary-numbers/.
“Imaginary Numbers.” 2024. Math Is Fun Advanced. Accessed January 11. https://www.mathsisfun.com/numbers/imaginary-numbers.html.
McBride, Martin. 2024. “Imaginary and Complex Numbers.” GraphicMaths. Accessed January 11. https://graphicmaths.com/pure/complex-numbers/imaginary-complex-numbers/.
Videos
A general solution to the cubic equation was long considered impossible, until we gave up the requirement that math reflect reality.
The featured image on this page is from the A brief history to imaginary numbers page on the BBC Science Focus website.