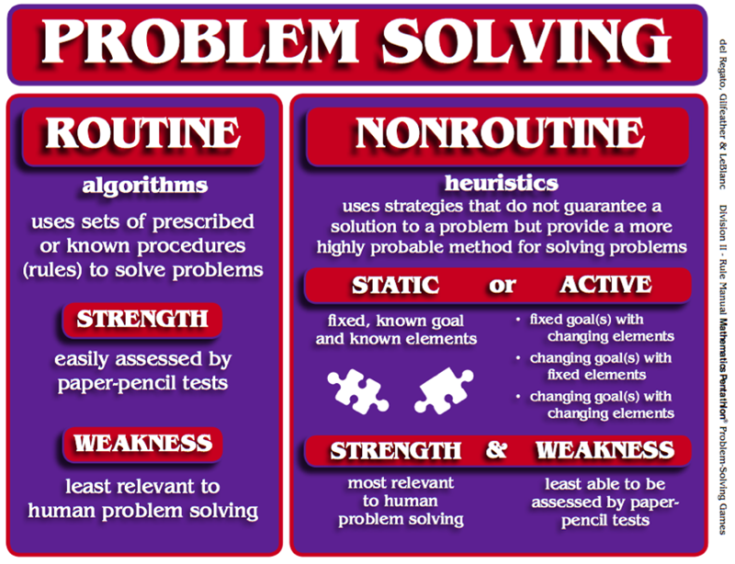
Nonroutine Problem Solving, stresses the use of heuristics [3] and often requires little to no use of algorithms. Unlike algorithms, heuristics are procedures or strategies that do not guarantee a solution to a problem but provide a more highly probable method for discovering a solution. Building a model and drawing a picture of a problem are two basic problem-solving heuristics. Studying end-of-game situations provides students with experiences in using the heuristics of reducing the problem to a similar but simpler problem and working a problem backwards, i.e. from its resolution to its initial state. Other heuristics include describing the problem situation, classifying information, and finding irrelevant information. [1]
There Are Two Categories of Nonroutine Problem Solving: Static and Active
Static-Nonroutine problems have a fixed, known goal and fixed, known elements that are used to resolve the problem. Solving a jigsaw puzzle is an example of a Static- Nonroutine problem. Given all pieces to a puzzle and a picture of the goal, learners are challenged to arrange the pieces to complete the picture. Various heuristics such as classifying the pieces by color, connecting the pieces that form the border, or connecting the pieces that form a salient feature to the puzzle, such as a flag pole, are typical ways in which people attempt to resolve such problems. [1]
Active-Nonroutine problems may have a fixed goal with changing elements, a changing goal or alternative goals with fixed elements, or changing or alternative goals with changing elements. The heuristics used in this form of problem-solving are known as strategies. People who study such problems must learn to change or adapt their strategies as the problem unfolds. [1]
What is non-routine problem-solving in math?
A non-routine problem is any complex problem that requires some degree of creativity or originality to solve. Non-routine problems typically do not have an immediately apparent strategy for solving them. Often times, these problems can be solved in multiple ways.
Incorporating non-routine problem solving into your math program is one of the most impactful steps you can take as an educator. By consistently allowing your students to grapple with these challenging problems, you are helping them acquire essential problem-solving skills and the confidence needed to successfully execute them. [2]
Step 1: Understand
This is a time to just think! Allow yourself some time to get to know the problem. Read and reread. No pencil or paper necessary for this step. Remember, you cannot solve a problem until you know what the problem is!
- Does the problem give me enough information (or too much information)?
- What question is being asked of me?
- What do I know and what do I need to find out?
- What should my solution look like?
- What type of mathematics might be required?
- Can I restate the problem in my own words?
- Are there any terms or words that I am unfamiliar with?
Step 2: Plan
Now it’s time to decide on a plan of action! Choose a reasonable problem-solving strategy. Several are listed below. You may only need to use one strategy or a combination of strategies.
- Draw a picture or diagram
- Make an organized list
- Make a table
- Solve a simpler related problem
- Find a pattern
- Guess and check
- Act out a problem
- Work backward
- Write an equation
- Use manipulatives
- Break it into parts
- Use logical reasoning
Step 3: Execute
Alright! You understand the problem. You have a plan to solve the problem. Now it’s time to dig in and get to work! As you work, you may need to revise your plan. That’s okay! Your plan is not set in stone and can change anytime you see fit.
- Am I checking each step of my plan as I work?
- Am I keeping an accurate record of my work?
- Am I keeping my work organized so that I could explain my thinking to others?
- Am I going in the right direction? Is my plan working?
- Do I need to go back to Step 2 and find a new plan?
- Do I think I have the correct solution? If so, it’s time to move on to the next step!
Step 4: Review
You’ve come so far, but you’re not finished just yet! A mathematician must always go back and check his/her work. Reviewing your work is just as important as the first 3 steps! Before asking yourself the questions below, reread the problem and review all your work.
- Is my answer reasonable?
- Can I use estimation to check if my answer is reasonable?
- Is there another way to solve this problem?
- Can this problem be extended? Can I make a change to this problem to create a new one?
- I didn’t get the correct answer. What went wrong? Where did I make a mistake?
References
[1] “Pentathlon Institute Active Problem-Solving”. 2023. mathpentath.org. https://www.mathpentath.org/active-problem-solving/.
[2] Tallman, Melissa. 2015. “Problem Solving In Math • Teacher Thrive”. Teacher Thrive. https://teacherthrive.com/non-routine-problem-solving/.
[3] A heuristic is a mental shortcut commonly used to simplify problems and avoid cognitive overload.
Additional Reading
“101 Great Higher-Order Thinking Questions for Math”. 2023. elementaryassessments.com. https://elementaryassessments.com/higher-order-thinking-questions-for-math/.
⭐ “Developing Mathematics Thinking with HOTS (Higher Order Thinking Skills) Questions”. 2023. saydel.k12.ia.us. https://www.saydel.k12.ia.us/cms_files/resources/Developing%20Mathematics%20Thinking%20with%20HOTS%20Questions%20(from%20classroom%20observations)PDF.pdf.
“Higher Order Thinking Skills in Maths”. 2017. education.gov.Scot. https://education.gov.scot/resources/higher-order-thinking-skills-in-maths/.
“How to Increase Higher Order Thinking”. 2023. Reading Rockets. https://www.readingrockets.org/topics/comprehension/articles/how-increase-higher-order-thinking.
⭐ I suggest that you read the entire reference. Other references can be read in their entirety but I leave that up to you.
