Contents
While taking the udemy Graph Theory course, TBS.
60. Cartesian Product
I pondered over the following question in Section 8, Lesson 60, Cartesian Product and wondered if there was an algebraic way to calculate the number of edges that is the result of the Cartesian product between the two graphs.
Question: How many edges does the graph that is the result of the Cartesian product between the two graphs have? Illustrate if needed.
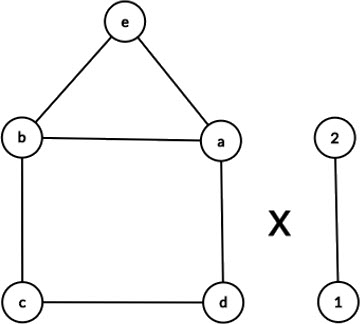
| Graph | Vertices | Edges |
|---|---|---|
| G1 | 5 | 6 |
| G2 | 2 | 1 |
The instructor used some simple examples to demonstrate how to determine the number of edges of the graph that is the result of the Cartesian product between the two graphs. Even these proved tedious to solve. After pondering the problem, I came up with the following formula to make the process more simple.
# edges = ( G1(v) * G2(e) ) + ( G2(v) * G1(e) )
Use the above formula and the information in the above table to calculate the number of edges of the graph that is the result of the Cartesian product between G1 and G2.
# edges = ( G1(v) * G2(e) ) + ( G2(v) * G1(e) )
# edges = ( 5 * 1 ) + ( 2 * 6 ) = 5 + 12 = 17
QED
This works for all Cartesian products between two planar graphs as shown in Algebraic graph theory.
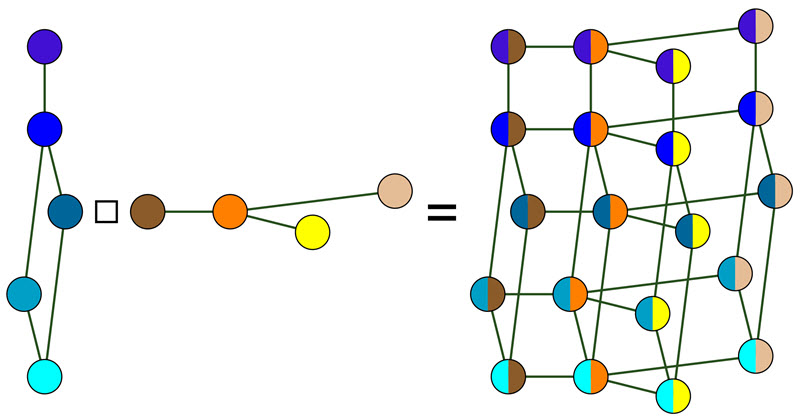
The featured image on this page is from the Wikipedia website.
Mathematical Mysteries 