A Fermi problem is a type of estimation challenge that aims to find a reasonable approximation for a quantity when exact data is unavailable or hard to obtain. These problems, named after physicist Enrico Fermi, involve breaking down complex questions into smaller, manageable parts and using reasonable assumptions and estimates to arrive at an answer, often within an order of magnitude.
Key Characteristics of Fermi Problems
- Estimation-based: The essence of a Fermi problem is making educated guesses and approximations to find a solution.
- Order-of-magnitude answers: The aim is not to find an exact answer, but rather an estimate that is accurate within a factor of two or three, or at least within the correct order of magnitude.
- Breaking down complexity: Fermi problems are solved by dividing a complex question into simpler, more manageable sub-problems.
- Assumptions and estimations: Reasonable assumptions and estimations are used to fill in gaps in knowledge and to simplify calculations.
- Emphasize reasoning: The process of logical thinking and making assumptions is just as important as the final numerical result.
Skills Needed
Many skills learned in math classes help solve Fermi Questions.
- Algebraic Expressions
- Critical Thinking!
- Draw a Picture, Diagram or Model
- Estimation
- Formulas
- Identify a Pattern
- Make a Table
- Measurement
- Problem Solving
- Solve a Simpler Related Problem
- Work Backwards
Example
How many piano tuners are there in Chicago?
- Estimate the population of Chicago.
- Estimate the fraction of this population that plays or has access to a piano.
- Estimate how often a piano needs to be tuned.
- Estimate how many pianos a tuner can service in a specific time period.
- Use these estimates to calculate the total number of piano tuners needed.
One Solution (Out of Many)
The key is to break the problem into smaller, manageable steps and make reasonable estimates for each step.
- Say 2.5 million people.
- If 20% play the piano, then there are 500,000 pianos.
- If a piano needs tuning once per year, then 500,000 pianos require tuning each year.
- If it takes 4 hours to tune a piano, then 2 million hours of work per year are needed for tuning pianos. Assume a tuner works a 40-hour week, 50 weeks a year.
- Then 2,000,000 hours per year divided by (40 x 50) hours per year per tuner equals 1,000 tuners are needed.
Summary
Fermi problems are useful for developing critical thinking, problem-solving, and approximation skills. They are used in various fields including science, engineering, and business to quickly assess situations and make informed decisions when precise data isn’t available. They are also often employed in job interviews to evaluate a candidate’s ability to think quickly and handle uncertainty.
Remember: The goal is not always to get an exact answer!
References
“5.6: Recognizing Patterns.” 2024. Mathematics LibreTexts. June 28, 2024. https://math.libretexts.org/Courses/Coalinga_College/Math_for_Educators_(MATH_010A_and_010B_CID120)/05:_Problem_Solving/5.06:_Recognizing_Patterns.
Ambati, Bharat. 2025. “Why Do Fermi Estimates Work?” Medium. June 12, 2025. https://medium.com/@bharatambati/why-do-fermi-estimates-work-7cf8beb819eb.
When Odysseus set sail for Ithaca, he didn’t have a GPS. On the other hand, he knew the sailor’s logic: “If the sun rises there, then Ithaca must be that way.”
Fermi estimates are something like this: we take our best guess at quantifying something. When exact answers aren’t available to us, when data is scattered or missing altogether, we use the next best thing: structured reasoning (based on some assumptions and guesses). You’ve probably done a Fermi estimate without even realising it: for example, guessing how many jellybeans are in a jar, estimating how long a road trip will take without checking Google Maps, or figuring out how many books fit in a library shelf.
Bangao, Kathlyn. 2025. “How to Break down Math Problems: A Simple Guide for Success – BrainMatters.” brainmatterslearning.com. March 2025. https://brainmatterslearning.com/how-to-break-down-math-problems/.
Bangao, Kathlyn. 2025. “How to Spot Patterns in Math – BrainMatters.” brainmatterslearning.com. March 4, 2025. https://brainmatterslearning.com/how-to-spot-patterns-in-math/.
Frederick, Cole. 2023. “Fermi Problems and the Art of Guessing.” Medium. Science Spectrum. December 10, 2023. https://medium.com/science-spectrum/fermi-problems-and-the-art-of-guessing-4ca9ab9f4513.
Schools go about teaching science in a very interesting way. Students are typically presented with a situation, usually written as a story problem, and they are expected to follow a set of rules to get the answer. Solving the problem often comes from knowing which equation to use or remembering some vocabulary words that apply to the situation. These are important parts of science; however, students are missing out on an essential skill: how to make educated guesses.
Cummins, Kevin. 2025. “An Excellent Collection of Fermi Problems for Your Class.” Innovative Teaching Ideas. July 15. https://innovativeteachingideas.com/blog/an-excellent-collection-of-fermi-problems-for-your-class/.
Physicist Enrico Fermi loved questions where exact data didn’t exist—so he built clever estimation hacks to get answers that were “close enough to be useful.” In today’s data‑rich world, that mindset is gold for students who must sift assumptions from facts. Let’s unpack how what a Fermi math problem is and how to handle them. Enrico Fermi is the father of “solving maths problems we will never know the exact answer to.” Such as how many leaves are on all the trees in Central Park. They are great for getting students to think mathematically and use problem-solving skills.
Fermi problems often require students to make reasonable assumptions and estimates about the situation to come up with an approximate answer. Students should be reminded of the need to be able to explain and justify what they did when coming up with their solutions. Students’ answers may differ from each other, but if students have made sensible estimates and assumptions, then the different answers should be “close” to each other.
“Fermi and the Problem Solved.” 2016. The Middle Road. July 15, 2016. https://drvcourt.wordpress.com/2016/07/15/fermi-and-the-problem-solved/.
Word problems in math textbooks often give much of the information needed to solve them. There is no mystery. Students walk away from a math course with the only skill acquired being the ability to decode the textbook. They are just swapping numbers and plugging in different information. As a result, the so-called problems are no longer problems. They are routine and predictable. The problems are too scaffolded and the students realize that it’s an exercise in futility. An insult to their intelligence. While practice is indeed a fundamental part of math, when problems are variations of the same one, the motivation to complete them is lost. They don’t see the point of it all.
“Fermi Estimate: Brilliant Math & Science Wiki.” 2025. Brilliant. Accessed August 13. https://brilliant.org/wiki/fermi-estimate/.
A Fermi estimate is one done using back-of-the-envelope calculations and rough generalizations to estimate values which would require extensive analysis or experimentation to determine exactly.
Gökçehan Pürsöken Coaching & Training. 2024. “Fermi Problems.” linkedin.com. July 20, 2024. https://www.linkedin.com/pulse/fermi-problems-gp%C3%BCrs%C3%B6ken-coaching-training-nj47f.
When preparing for a job interview, most candidates focus on rehearsing their responses to common interview questions about their background, skills, and career goals. However, there is another type of question that is becoming increasingly common in interviews – the Fermi problem.
Gupta, Saurabh. 2022. “Software System Design: Back-of-Envelope Calculations.” Medium. September 6, 2022. https://medium.com/@saurabh.engg.it/software-system-design-back-of-envelope-calculations-8f2d9d0f4edd.
System design is a process of designing the elements of a software system, such as components, architecture, interfaces, modules, types of databases, etc., and then defining the mechanism of how the different components interact with each other. This includes both data flow & data access.
Landry, Benjamin. 2020. “What Is the Fermi Problem-Solving Strategy?” Medium. Medium. December 29. https://benjaminlandry.medium.com/what-is-the-fermi-problem-solving-strategy-9fee916fa44a.
A fermi problem is a category of problems that require estimations and assumptions to solve. It tends to be creative or out-of-the-box questions. To fermi-ize a problem involves solving a problem with the fermi problem-solving strategy. The essence is to breakdown a large and broad question into its smallest elements. At which time, each element would be solved for. Then, all the elements would be accumulated to produce a conclusion.
“Lesson Plan: Fermi Challenge.” 2025. National Environmental Satellite, Data, and Information Service. 2025. https://www.nesdis.noaa.gov/about/k-12-education/jpss-education/lesson-plan-fermi-challenge.
Fermi problems, named after physicist Enrico Fermi, are open-ended problems where students have to make assumptions, estimates, and educated guesses to creatively solve a problem. These complicated problem-solving exercises help students gain confidence in thinking like an engineer or scientist. These questions can be a fun way to encourage students to work on math problems as a group and can be tailored to a variety age levels.
“Problem Solving: Simplify the Problem.” 2007. TeacherVision. March 15, 2007. https://www.teachervision.com/mathematics/problem-solving-simplify-the-problem.
Tanner, Becca. “Fermi Problems Part 1: Envelopes at the Ready!” 2022. TOM ROCKS MATHS. January 10, 2022. https://tomrocksmaths.com/2022/01/10/fermi-problems-part-1-envelopes-at-the-ready/.
What if I told you that you could solve some of the most seemingly complex mathematical problems with little more than, well, the back of an envelope (and a healthy bit of critical thinking)? I wouldn’t blame you for feeling slightly skeptical, but stick with me, because what lies ahead is the opportunity to dive into the prodigious realm of problem solving: from the strength of atomic bombs to the mass of the ocean, and ultimately, to the quest for extraterrestrial life.
Tanner, Becca. “Fermi Problems Part 2: Don’t Sweat the Small Stuff.” 2022. TOM ROCKS MATHS. January 31, 2022. https://tomrocksmaths.com/2022/01/31/fermi-problems-part-2-dont-sweat-the-small-stuff/.
The best way to understand Fermi Problems is to try one. So, where’s a better place to start than estimating the total mass of all the oceans on Planet Earth? Of course, we know it’s going to be a huge number, but exactly how large? Believe it or not, this is a relatively simple problem, using formulas you probably learned in school science classes. Before we begin, though, there are some helpful tips to remember so we can successfully solve any Fermi Problem.
Tanner, Becca. “Fermi Problems Part 3: Where Is Everybody?” 2022. TOM ROCKS MATHS. February 7, 2022. https://tomrocksmaths.com/2022/02/07/fermi-problems-part-3-where-is-everybody/.
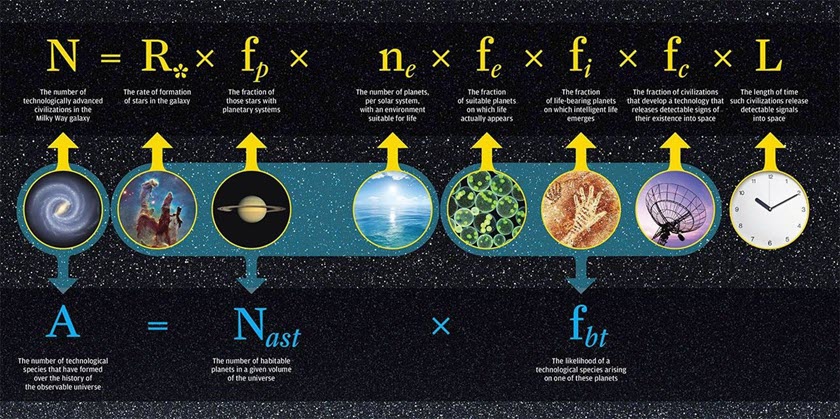
So far we have seen a whole bunch of problems that can be solved using Fermi Estimation, but what about one of the biggest questions of them all: is there intelligent life somewhere else in the Milky Way galaxy? In 1961, Frank Drake tried to answer exactly that. Although written only to stimulate discussion, rather than to actually quantify the number of extraterrestrial civilizations, the Drake Equation is perhaps one of the most famous Fermi Problems ever written.
“WEST VIRGINIA DEPARTMENT of EDUCATION GRADE 6 MATHEMATICS Fermi Problems.” n.d. Accessed August 13, 2025. https://wvde.us/sites/default/files/2020/08/Fermi-Problems-Task-Guide-Final1-June-29.pdf.
In this three-part math task, students use their knowledge of ratios and ratio reasoning to solve an unfamiliar, Fermi-style problem. A Fermi problem is an estimation problem designed to teach approximation of extreme calculations. The classic Fermi problem is, “How many piano tuners are there in Chicago?” Students might be more interested in, “How many sheets of paper would be in a stack that reaches from the floor to the ceiling of our classroom?”
Videos
What Is A Fermi Problem? Have you ever encountered a question that seems impossible to answer? In this engaging video, we discuss the fascinating concept of Fermi problems and how they can be tackled. We will explain what a Fermi problem is and how it encourages logical reasoning and estimation skills. By breaking down complex questions into smaller, manageable parts, you can arrive at a reasonable approximation even without extensive data. We will illustrate this with an example involving piano tuners in New York City, demonstrating how to make assumptions and use basic math to estimate an answer. This method is not only applicable to scientific inquiries but also to everyday situations, making it a versatile tool for enhancing analytical thinking. Whether you’re a student, a professional, or just someone curious about problem-solving techniques, this video will provide you with practical approaches to tackle seemingly impossible questions. Join us as we unravel the art of estimation and reasoning. Don’t forget to subscribe to our channel for more educational content on the history of science and critical thinking strategies.
In physics or engineering education, a Fermi problem, or order-of-magnitude problem is an estimation problem designed to teach dimensional analysis or approximation of extreme scientific calculations, and such a problem is usually a back-of-the-envelope calculation. The estimation technique is named after physicist Enrico Fermi as he was known for his ability to make good approximate calculations with little or no actual data.
Enrico Fermi (29 September 1901 – 28 November 1954) was an Italian (later naturalized American) physicist and the creator of the world’s first nuclear reactor, the Chicago Pile-1. He has been called the “architect of the nuclear age” and the “architect of the atomic bomb”. He was one of very few physicists to excel in both theoretical physics and experimental physics. Fermi was awarded the 1938 Nobel Prize in Physics for his work on induced radioactivity by neutron bombardment and for the discovery of transuranium elements. With his colleagues, Fermi filed several patents related to the use of nuclear power, all of which were taken over by the US government. He made significant contributions to the development of statistical mechanics, quantum theory, and nuclear and particle physics.
Fermi problems typically involve making justified guesses about quantities and their variance or lower and upper bounds. An example of this is Enrico Fermi’s estimate of the strength of the atomic bomb that detonated at the Trinity test, based on the distance traveled by pieces of paper he dropped from his hand during the blast. Fermi’s estimate of 10 kilotons of TNT was well within an order of magnitude of the now-accepted value of 21 kilotons. But possibly the most famous Fermi Question is the Drake equation, which seeks to estimate the number of intelligent civilizations in the galaxy. The basic question of why, if there were a significant number of such civilizations, ours has never encountered any others is called the Fermi paradox. Scientists often look for Fermi estimates of the answer to a problem before turning to more sophisticated methods to calculate a precise answer.
This provides a useful check on the results. While the estimate is almost certainly incorrect, it is also a simple calculation that allows for easy error checking, and to find faulty assumptions if the figure produced is far beyond what we might reasonably expect. By contrast, precise calculations can be extremely complex but with the expectation that the answer they produce is correct. The far larger number of factors and operations involved can obscure a very significant error, either in mathematical process or in the assumptions the equation is based on, but the result may still be assumed to be right because it has been derived from a precise formula that is expected to yield good results. Without a reasonable frame of reference to work from it is seldom clear if a result is acceptably precise or is many degrees of magnitude (tens or hundreds of times) too big or too small. The Fermi estimation gives a quick, simple way to obtain this frame of reference for what might reasonably be expected to be the answer.
Fermi estimates generally work because the estimations of the individual terms are often close to correct, and overestimates and underestimates help cancel each other out. That is, if there is no consistent bias, a Fermi calculation that involves the multiplication of several estimated factors (such as the number of piano tuners in Chicago) will probably be more accurate than might be first supposed. The power of estimation is amazing. The ability to construct close-to-accurate measurements with limited information is such a useful skill to have because it’s encountered so often in the real world. This proves the high efficiency of the Fermi Problem.
Have you ever tried to guess how many pieces of candy there are in a jar? Or tackled a mindbender like: “How many piano tuners are there in Chicago?” Physicist Enrico Fermi was very good at problems like these — learn how he used the power of 10 to make amazingly fast estimations of big numbers.
Data analytics and data science interviews for companies like Google, McKinsey, Amazon and more always ask Fermi Problems. But why? How can you learn how to solve them and get ahead in your data career. In this tutorial find out how Fermi estimates combined with a knowledge of landmark numbers can help you get further in your career.
Notes
Critical Thinking
Critical thinking is the ability to analyze information objectively and make a reasoned judgement. It involves the evaluation of sources, such as data, facts, observable phenomena and research findings.
Critical thinking is the active and skillful process of analyzing, evaluating, and synthesizing information obtained from various sources, such as observation, experience, and reasoning. It is a disciplined approach that assists individuals in making informed decisions and solving problems effectively. Critical thinking is crucial in many areas, including education, science, and everyday life, as it enables people to assess the credibility of information, recognize biases, and develop sound arguments.
Key Components of Critical Thinking
- Analysis: Breaking down complex information into manageable parts to understand its structure and meaning.
- Evaluation: Assessing the credibility and relevance of information sources and arguments.
- Synthesis: Combining different pieces of information to form a coherent understanding or new perspective.
- Reflection: Thinking about one’s own thought processes and biases to improve reasoning and decision-making.
Draw a Picture, Diagram or Model
Drawing a picture, diagram, or model is one of the most common problem-solving strategies. Often, you need to create a visual representation to fully understand the problem. By drawing a picture, diagram, or model, you can visualize the problem, which helps them comprehend it better and consider the next steps in solving it.
The process of drawing a picture or diagram to solve a math problem involves several key steps:
- Read and Understand the Problem: Identify the problem statement and understand what is being asked.
- Visualize the Problem: Use the picture or diagram to visualize the problem and its components.
- Organize Information: Arrange the information in the diagram to make it easier to understand and solve.
- Identify Relationships: Look for relationships between the parts of the problem represented in the diagram.
- Solve the Problem: Use the information and relationships in the diagram to solve the problem.
Estimation
Estimation in math refers to the process of finding a value that is close to the actual value, even if it is not exact. This approach is helpful when exact answers are unnecessary or when precise measurements or calculations are challenging. Estimation can involve rounding numbers, using compatible numbers, or applying various mental math strategies.
Methods of Estimation
- Rounding: Rounding numbers to the nearest 10, 100, or other place values simplifies calculations. For example, to estimate 78 + 23, you could round 78 to 80 and 23 to 20, making the estimated sum 100.
- Compatible Numbers: Choosing numbers that are easy to calculate with mentally, such as multiples of 5 or 10, can be helpful for estimation. For example, to estimate 24 x 6, you could use 25 x 6, which is 150.
- Front-End Estimation: In this method, you focus on the leftmost digit(s) of the numbers to get a quick estimate. For example, to estimate 372 + 581, you could add 300 + 500 = 800.
Identify a Pattern
Recognizing patterns is one of the most important skills in math. Whether you’re learning algebra, geometry, or even statistics, being able to find and understand patterns can make tough problems much easier.
In math, a pattern is a repeated sequence or a set of rules that shows how something is organized. It could be a series of numbers, shapes, or operations that follow a predictable path. When you find these patterns, you can figure out what comes next and solve problems faster.
Identifying patterns to solve a math problem involves several key steps and strategies:
- Recognizing Repeated Sequences: Patterns can be found in sequences of numbers, shapes, or operations that follow a specific rule. For example, arithmetic sequences add a constant difference, while geometric sequences multiply by a constant factor.
- Visualizing Patterns: Patterns can appear in visual forms, such as shapes or arrangements. Understanding symmetry, tessellations, and fractals can help in identifying these patterns.
- Predicting Future Events: By recognizing patterns, you can predict what comes next in a sequence, which is crucial for solving problems in sequences and series.
- Simplifying Problems: Patterns can reduce the complexity of a problem by revealing relationships that are not immediately obvious, making it easier to solve.
- Enhancing Understanding: Recognizing patterns deepens your understanding of mathematical concepts and relationships between different problems and solutions.
Make a Table
To create a table for solving a math problem, start by understanding the problem and identifying the necessary information. Next, design a table with appropriate headings relevant to the context of the problem. Input the known information into the table. Look for patterns or relationships within the data. Extend the table based on these patterns to find the solution. Finally, interpret the results in the context of the original problem.
- Understand the Problem: Carefully analyze the problem to identify the main question and available information needed to find the answer.
- Set up the Table:
- Draw a table with rows and columns.
- Label the rows and columns with appropriate headings based on the context of the problem. For example, if the problem involves time and distance, you might have columns for “Time” and “Distance”.
- Choose a reasonable number of rows based on the problem’s complexity and the amount of data you anticipate needing.
- Enter the Known Information:
- Fill in the table with the data that is explicitly provided in the problem.
- If the problem involves a relationship between variables, like a linear equation, you might need to calculate some values to fill in the table.
- Identify Patterns:
- Look for relationships or patterns in the numbers within the table.
- For example, you might notice that each number in a column increases by a fixed amount, or that two columns have a consistent ratio.
- Extend the Table:
- Based on the identified pattern, extend the table to include more values.
- This might involve continuing a sequence, applying a formula, or using the relationship between variables to find missing values.
- Find the Solution:
- Once the table is extended, locate the answer to the problem within the table.
- The solution might be a specific value in a cell, or it might be a relationship between values that you can use to answer the question.
- Check and Interpret:
- Verify that the solution makes sense in the context of the problem.
- Ensure that you have answered the original question and that your answer is reasonable.
Problem Solving
The steps involved in problem-solving in math, as outlined by George Pólya, are understand the problem, devise a plan, carry out the plan, and look back. This process helps break down complex problems into manageable steps for practical solutions.
- Understand the Problem
- Carefully read the problem multiple times to ensure you grasp all the information and the specific question asked.
- Identify the given information (what you know) and what you need to find (the unknown).
- Restate the problem in your own words to confirm your understanding.
- Consider drawing a diagram or picture to visualize the problem.
- Devise a Plan
- Choose appropriate strategies to solve the problem, such as:
- Looking for patterns.
- Examining related problems or simpler cases.
- Creating a table, diagram, or chart.
- Writing an equation.
- Using guess and check.
- Working backward.
- Identifying subgoals.
- Translate the problem into a mathematical equation or expression.
- Choose appropriate strategies to solve the problem, such as:
- Carry Out the Plan:
- Solve the problem using the chosen strategy and mathematical operations.
- Perform the necessary calculations accurately.
- Look Back
- Check your solution by substituting it back into the original problem or by using inverse operations.
- Ensure your answer makes sense in the context of the problem.
- Consider if there might be other ways to solve the problem.
Solve a Simpler Related Problem
Simplifying a mathematics problem is a strategy that often is used along with other problem-solving strategies. When a problem is too complex to solve in one step, it often helps to divide it into simpler problems and solve each one separately. Creating a simpler problem from a more complex one may involve rewording the problem; using smaller, simpler numbers; or using a more familiar scenario to understand the problem and find the solution.
To solve a simpler related problem in math, follow these steps:
- Read the problem carefully: Ensure you understand the question and identify the goal of the problem.
- Identify what you know and what you don’t know: Make a list of the information you have and the information you need to find.
- Break it down into smaller parts: Look for relationships and understand the operations needed to solve the problem.
- Solve step by step: Write down each calculation clearly and check your answer to ensure it makes sense.
- Check your answer: Plug your answer back into the original problem to see if it works.
- These steps can help you tackle math problems more effectively and build your confidence in solving them.
Work Backwards
To solve math problems using the working backwards method, follow these steps:
- Understand the Concept: Start at the end of the problem and work through to the beginning, reversing the operations to find the solution.
- Identify the Final Outcome: Determine what the final answer or result should be.
- Reverse the Steps: Undo each step or operation that leads to the final outcome, working backwards through the problem.
- Practice with Examples: Use word problems and examples to practice applying the working backwards strategy.
- Engage in Activities: Participate in activities that require using the working backwards method to reinforce understanding.
The featured image on this page is from the Innovative Teaching Ideas website.
