Factoring Trinomials

Factoring truly can be one of the most challenging skills that students learn in secondary mathematics. To make matters worse, it is used very often in more complex mathematics. This is why it is so important that teachers explore how to teach factoring in ways that support student learning. There are so many different factoring methods out there that it is important to think about the best one for you. Whether you are a teacher or a student, finding a strategy that helps you feel comfortable is important. [1]

Contents

Background

In mathematics, monomials, binomials, trinomials and polynomials are all algebraic expressions. The expressions that are represented using unknown variables, constants and coefficients, are called algebraic expressions. A variable can take any value, it is not fixed but a constant is a fixed value.

Trinomials

A trinomial is an expression which is composed of exactly three terms.

The parts of algebraic expressions that are separated by addition or subtraction, are called terms. The number of terms decides the type of expression, whether it is a monomial, binomial, trinomial or polynomial. These terms are made of a product of variables and coefficients that are added together to form expressions. [2]

Perfect Square Trinomial

A perfect square trinomial is a mathematical expression formed by squaring a binomial. It follows the pattern ax² + bx + c, where (a), (b), and (c) are real numbers, and (a) is not equal to zero. It also meets the condition b² = 4ac. Perfect Square Trinomials Formula are,

(ax)² + 2abx + b² = (ax + b)²
(ax)² – 2abx + b² = (ax – b)²

To recognize a perfect square trinomial, follow these steps:

Check Form: Look at the expression, and if it’s in the form (ax² + bx + c), it could be a perfect square trinomial.

Verify Condition: Confirm if the condition b² = 4ac is met. Here, (b) is the coefficient of the linear term, and (a) and (c) are the coefficients of the squared and constant terms, respectively.

Compare with Formula: See if the expression matches the structure of (ax + b)² or (ax – b)². If it does, then it’s a perfect square trinomial. [3]

Quadratic Trinomial

A quadratic trinomial is a specific kind of mathematical expression containing both variables and constants. It appears in the form (ax² + bx + c), where (x) is the variable, and (a), (b), and (c) are real numbers that are not zero. Here, (a) is called the leading coefficient, (b) is the linear coefficient, and (c) is the additive constant.

There’s a key aspect related to quadratic trinomials, called the discriminant (D), expressed as (D = b² – 4ac). The discriminant helps categorize different cases of quadratic trinomials. By evaluating (D), you can understand more about the nature of the quadratic expression.

If a quadratic trinomial, which involves just one variable, equals zero, it transforms into what’s known as a quadratic equation, represented as (ax² + bx + c = 0). In simpler terms, when a quadratic trinomial takes this form, it becomes a quadratic equation. [3]

Factoring Trinomials

Factoring trinomials means transforming a mathematical expression from having three terms to having two terms. A trinomial is a polynomial with three terms, generally represented as ax²+bx+c, where a and b are coefficients, and c is a constant.

To factor a trinomial, two integers, often denoted as r and s, are selected such that their sum equals b, and their product equals ac. Trinomial is then rewritten as ax²+ rx + sx + c. Using distributive property, the polynomial is then factored. Now the trinomial is written as (x + r)(x + s). [3]

The Factoring Decision Tree (Math By The Pixel Way)

Giving students something visual that helps them see the decisions they have available to them is very helpful and makes the whole process much less stressful for them. [1]

Step 1: Check for a Greatest Common Factor

Remember if the leading coefficient is negative, so is the GCF. Use the distributive rule to extract the GCF.

−10y⁴ − 55y³ − 60y²

-5y² (2y² +11y + 12)

Step 2: Is the Quadratic Expression a Trinomial?

A trinomial is an expression which is composed of exactly three terms.

Differences of Squares?

When you learn to factor quadratics, there are three other formulas that they usually introduce at the same time. The first is the “difference of squares” formula.

Remember from your translation skills that a “difference” means a “subtraction”. So a difference of squares is something that looks like x² − 4. That’s because 4 = 2², so we really have x² − 2², which is a difference of squares. [5]

To factor this, I’ll start by writing my parentheses, in the same way as usual for factoring:

x² − 4 = (x )(x )

For this quadratic factorization, I need factors of −4 that add up to zero, so I’ll use −2 and +2:

x² − 4 = (x − 2)(x + 2)

(Review Factoring Quadratics, if the steps in this example didn’t make sense to you.)

Difference-of-Squares Formula

For a difference of squares a² − b², the factorization is: (a − b)(a + b)

Grouping?

Another way to factor trinomials of the form 𝑎𝑥²+𝑏𝑥+𝑐 is the “ac” method. (The “ac” method is sometimes called the grouping method.) The “ac” method is actually an extension of the methods used in factoring trinomials with a leading coefficient of one. This method is very structured (that is step-by-step), and it always works!

Factor using the ‘ac’ method: 6x²+7x+2. [4]

*How to Factor Trinomials using the “ac” Method – LibreTexts*

Step 3: Check the Leading Coefficient

The leading coefficient is the number in front of the x term that has an exponent of two (if you are working with a quadratic expression).

When the Leading Coefficient Is Equal to One

If the leading coefficient is equal to one, we are working with a simple case of trinomial factoring. We can start this process with decomposition, or the “splitting the middle term” process. [1]

To Factor the form : ax² + bx + c	Factor : 6x² + 19x + 10
1) Find the product of 1st and last term (a x c).	6 x 10 = 60
2) Find the factors of 60 in such way that addition or subtraction of that factors is the middle term (19x) (Splitting of middle term)	15 x 4 = 60 and 15 + 4 = 19 (Some teachers will use a factor tree to help students find the different factors that work for this step.)
3) Write the center term using the sum of the two new factors, including the proper signs. Remember that negative numbers are important to consider as well!	6x² + 15x + 4x + 10
4) Group the terms to form pairs – the first two terms and the last two terms. Factor each pair by finding common factors.	3x(2x + 5)+ 2(2x + 5)
5) Factor out the shared (common) binomial parenthesis.	(3x + 2) (2x + 5)

Quadratic Factorization Using Splitting of Middle Term

When the Leading Coefficient Is Not Equal to One

If the leading coefficient is anything other than one, I direct my students to the right side of the decision tree above, i.e., Differences of Squares and Grouping. The same process as above can be applied to tackle a problem like this. I have my own crazy trick for factoring these sorts of trinomials that you sort of have to see to believe. You can check out a video of my trinomial factoring process. [1]

Step 4: Checking Your Work

After successfully factoring a quadratic polynomial, I always make sure to check if my answer makes sense. The only way to do this is to apply the distributive property for binomials (sometimes known as FOIL). This process allows us to take a product of binomials and write them in standard form. If you see that your standard form expression is the same as the original trinomial, you know that your factored expression is correct! [1]

Box Method (Magic Squares)

Factoring using the “box” or “grid” method is a great alternative to factoring trinomial by grouping method when the leading coefficient, 𝑎a, is not equal to 1 or −1. [7]

a ≠ 1 and a ≠ -1
ax² + bx + c

TIP: Before you can apply the general steps below, make sure to first take out common factors among the coefficients of the trinomial. Otherwise, the method will not work and therefore will give us a wrong answer. In other words, for this to work, the Greatest Common Factor (GCF) of a, b, and c in 𝑎𝑥² + 𝑏𝑥 + 𝑐 must be 1.

Step 1: Multiply the leading coefficient and the constant term (number without variable), i.e.,

a × c

Step 2: Find two numbers such that the product is equal to a·c and the sum is equal to the middle coefficient, b. Let “n” and “m” be the two numbers satisfying the two conditions.

n × m = a × c
and
n + m = b

Step 3: Create a 2×2 grid and place the following terms in the right boxes:

Place the first term in the upper left box.
Place the constant term in the lower right box.
Place the numbers you found in step 2 in the remaining empty boxes. This time, it doesn’t matter where you place them. Make sure that you attach a variable x to each number.

Step 4: Find the Greatest Common Factor on each row and column. Place them outside the box. Take the sign of the term closest to it.

where: q, r, s and t are GCFs

Step 5: The factors of the trinomial are coming from the outside terms.

ax² + bx + c = (qx + r)(sx + t)

See Examples of How to Factor a Trinomial using the “Box” Method on the ChiliMath website.

You may also be interested in these related math lessons or tutorials:

Factoring Trinomial where a=1
Factoring Trinomial where a>1

Perfect Square

A perfect square trinomial is defined as an algebraic expression that is obtained by squaring a binomial expression. It is of the form ax² + bx + c. Here a, b, and c are real numbers and a ≠ 0. For example, let us take a binomial (x+4) and multiply it to (x+4). The result obtained is x² + 8x + 16. A perfect square trinomial can be decomposed into two binomials and the binomials when multiplied with each other gives the perfect square trinomial. Perfect square trinomial generally has the pattern of a² + 2ab + b² or a² – 2ab + b². [8]

Given a perfect square trinomial, factor it into the square of a binomial. [9]

Confirm that the first and last term are perfect squares.
Confirm that the middle term is twice the product of 𝑎𝑏.
Write the factored form as (a+b)².

Diamond Method

Important

Remember that the first step in any factoring is to look at each term and factor out the greatest common factor.

For example: 3x² + 6x + 12 = 3(x² + 2x + 4) AND 5x² + 10x = 5x(x + 2)
If the leading coefficient is negative, always factor out the negative.

For example: -2x² – x + 1 = -1(2x² + x – 1) = -(2x² + x – 1)

Factor 2x² + 11x + 15 using the Diamond Method. [10]

Step 1: Multiply the coefficient of the x² term (+2) and the constant (+15) and place this product (+30) in the top quarter of a large “X.”

Step 2: Place the coefficient of the middle term in the bottom quarter of the “X.” (+11)

Step 3: List all factors of the number in the top quarter of the “X.”

Step 4: Identify the two factors whose sum gives the number in the bottom quarter of the “X.” (5 ∙ 6 = 30 and 5 + 6 = 11) and place these factors in the left and right quarters of the “X” (order is not important).

Step 5: Break the middle term of the original trinomial into the sum of two terms formed using the right and left quarters of the “X.” That is, write the first term of the original equation, 2x² , then write 11x as + 5x + 6x (the numbers from the “X”), and finally write the last term of the original equation, +15 , to get the following 4-term polynomial:

2x² + 11x + 15 = 2x² + 5x + 6x + 15

Step 6: Factor by Grouping:

Group the first two terms together and the last two terms together.

Factor out common factors from each group.

Factor out the common binomial factor.

Quadratic Equation

See the Quadratic Equation webpage.

A Quadratic Formula Calculator, on the CalculatorSoup website, can be used to solve a second-order polynomial equation such as ax² + bx + c = 0 for x, where a ≠ 0, using the quadratic formula. The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex roots.

Why Do We Factor Polynomials?

Factoring is a useful technique for solving polynomial equations. By breaking a polynomial down into smaller factors, we can often simplify the equation and find the solutions more easily. [11]

Just as whole numbers can be factored into a product prime numbers, polynomials too can be factored into simpler pieces. Prime polynomials are usually called “irreducible polynomials”.

They are especially important in solving equations. Each irreducible factor of a polynomial tells you a solution. (In some cases, they actually tell you some pair of complex numbers is a solution, but no matter).

For instance, if I know that x² – 5x + 6 = (x – 2)(x – 3), I suddenly know how to solve x² – 5x + 6 = 0. The solutions are x=2 and x=3. (This follows from something we call the zero-product property: if two numbers multiplied together is 0, then one of those number is 0).

The best situation (and one you see very often in algebra 2) is when a polynomial factors into linear factors. That is, your polynomial looks like (x – a)(x – b)(x – c) or something similar. Each factor is of the form (x – r) for some number r. Essentially, when you have factored a polynomial into linear factors, you know all of its solutions.

You can also interpret the solutions graphically. If (x – r) is a factor of a polynomial, then you know the graph of the polynomial passes through the point x = r.

So for instance, if you want a polynomial which passes through the x-axis at the points x = 0, 1, 2, 3, and 4, you could use x(x – 1)(x – 2)(x – 3)(x – 4).

An intriguing thing about factoring… both for polynomials and for whole numbers, is that it is hard to factor, while the inverse process (say, going from (x – 1)(x + 1) to x² – 1) is sometimes tedious, but ultimately not so bad. Ultimately, this asymmetry of difficulty is the basis of all cryptographic systems we use. [12]

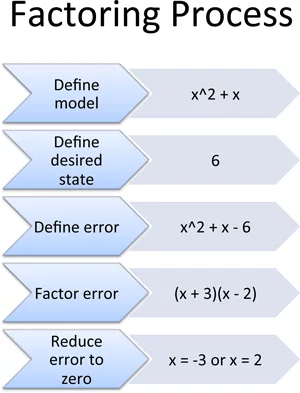
I’ve wondered about the real purpose of factoring for a long, long time. In algebra class, equations are conveniently set to zero, and we’re not sure why. Here’s what happens in the real world:

Define the model: Write how your system behaves (x² + x)
Define the desired state: What should it equal? (6)
Define the error: The error is its own system: Error = actual – desired (i.e., x² + x – 6)
Factor the error: Rewrite the error as interlocking components: (x + 3)(x – 2)
Reduce the error to zero: Zero out one component or the other (x = -3, or x = 2).

When error = 0, our system must be in the desired state. We’re done!

Algebra is pretty darn useful:

Our system is a trajectory, the “desired state” is the target. What trajectory hits the target?
Our system is our widget sales, the “desired state” is our revenue target. What amount of earnings hits the goal?
Our system is the probability of our game winning, the “desired state” is a 50-50 (fair) outcome. What settings make it a fair game?

The idea of “matching a system to its desired state” is just one interpretation of why factoring is useful. [13]

FOIL

FOIL is a mnemonic for the standard method of multiplying two binomials, hence the method may be referred to as the FOIL method.

The word FOIL is an acronym for the four terms of the product: [6]

First (“first” terms of each binomial are multiplied together)
Outer (“outside” terms are multiplied—that is, the first term of the first binomial and the second term of the second)
Inner (“inside” terms are multiplied—second term of the first binomial and first term of the second)
Last (“last” terms of each binomial are multiplied)

The general form is:

References

[1] Jordan. 2024. “How to Teach Factoring Trinomials (The Best Method!).” Math By The Pixel. May 23. https://mathbythepixel.com/how-to-teach-factoring/.

[2] “Monomials, Binomials, Trinomials and Polynomials.” 2021. BYJUS. BYJU’S. July 13. https://byjus.com/maths/monomials-binomials-trinomials-and-polynomials/.

[3] “Trinomials: Definition, Formula, Types, and Examples.” 2024. GeeksforGeeks. GeeksforGeeks. May 30. https://www.geeksforgeeks.org/trinomials/.

[4] “6.3: Factor Trinomials.” 2024. Mathematics LibreTexts. Libretexts. February 19. https://math.libretexts.org/Workbench/Intermediate_Algebra_2e_(OpenStax)/06%3A_Factoring/6.03%3A_Factor_Trinomials.

[5] Stapel, Elizabeth. 2024. “Special Factoring: Differences of Squares.” Purplemath. Accessed June 19. https://www.purplemath.com/modules/specfact.htm.

[6] “Foil Formula Algebra: What Is the Foil Method in Math.” 2022. BYJUS. BYJU’S. https://byjus.com/foil-formula/.

[7] Estela, Mike. 2023. “Factoring Trinomial: Box Method.” ChiliMath. December 15. https://www.chilimath.com/lessons/intermediate-algebra/factoring-trinomial-box-method/.

[8] “Perfect Square Trinomials – Definition, Factorization, Formula.” 2024. Cuemath. Accessed June 26. https://www.cuemath.com/algebra/perfect-square-trinomial/.

[9] Abramson, Jay. 2024. “1.5 Factoring Polynomials – Algebra and Trigonometry.” OpenStax. OpenStax. Accessed June 26. https://openstax.org/books/algebra-and-trigonometry/pages/1-5-factoring-polynomials.

Learning Objectives
– Factor the greatest common factor of a polynomial.
– Factor a trinomial.
– Factor by grouping.
– Factor a perfect square trinomial.
– Factor a difference of squares.
– Factor the sum and difference of cubes.
– Factor expressions using fractional or negative exponents.

[10] “The Diamond Method of Factoring a Quadratic Equation”. 2024. Allan Hancock College. Accessed June 26. https://www.hancockcollege.edu/mathcenter/documents/Diamond%20Method%20of%20Factoring.pdf.

[11] “Polynomial factorization: FAQ (Article).” 2024. Khan Academy. Khan Academy. Accessed June 19. https://www.khanacademy.org/math/algebra2/x2ec2f6f830c9fb89:poly-factor/x2ec2f6f830c9fb89:geo-series/a/polynomial-factorization-faq.

[12] “What is the purpose of factoring a polynomial? What is factoring?” 2024. reddit. reddit. Accessed June 26. https://www.reddit.com/r/math/comments/508qta/comment/d725gc7/.

[13] “Understanding Algebra: Why Do We Factor Equations?” 2024. BetterExplained. Accessed June 26. https://betterexplained.com/articles/understanding-algebra-why-do-we-factor-equations/.

Additional Reading

Factoring Trinomials

“6.2: Factoring Trinomials of the Form x²+bx+c.” Mathematics LibreTexts. Libretexts. October 6. https://math.libretexts.org/Bookshelves/Algebra/Beginning_Algebra/06%3A_Factoring_and_Solving_by_Factoring/6.02%3A_Factoring_Trinomials_of_the_Form_x_bx_c.

“Difference of Squares | Factoring Quadratics (Article).” 2024. Khan Academy. Khan Academy. Accessed June 19. https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:quadratics-multiplying-factoring/x2f8bb11595b61c86:factor-difference-squares/a/factoring-quadratics-difference-of-squares.

Estela, Mike. 2023. “Factoring Trinomial A=1.” ChiliMath. December 5. https://www.chilimath.com/lessons/intermediate-algebra/factoring-trinomial-easy-case/.

Estela, Mike. 2023. “Factoring Trinomial A≠1.” ChiliMath. December 4. https://www.chilimath.com/lessons/intermediate-algebra/factoring-trinomial-hard-case/.

“Factoring Trinomials – Definition, Rules, Methods, Formula, Examples.” 2024. CUEMATH. Accessed June 26. https://www.cuemath.com/algebra/factoring-trinomials/.

Factoring trinomials is converting an algebraic expression from a trinomial expression to a binomial expression. A trinomial is a polynomial with three terms with the general expression as ax² + bx + c, where a and b are coefficients and c is a constant.

“Factoring Trinomials: 4 Easy Methods.” 2024. SchoolTube. June 20. https://www.schooltube.com/factoring-trinomials-4-easy-methods/.

Factoring trinomials is a fundamental skill in algebra that allows you to express a polynomial as a product of simpler expressions. It’s a crucial step in solving quadratic equations, simplifying expressions, and understanding the behavior of functions. This blog post will guide you through four easy methods to factor trinomials, equipping you with the tools to master this essential skill.

“Polynomials (Definition, Types and Examples).” 2023. BYJUS. BYJU’S. October 3. https://byjus.com/maths/polynomial/.

“Trinomials – Definition, Types, Formulas, Examples.” 2024. examples.com. Examples.com. May 22. https://www.examples.com/maths/trinomials.html.

“Trinomials – Formula, Examples, Types.” 2024. CUEMATH. Accessed June 19. https://www.cuemath.com/algebra/trinomial/.

“Trinomials: Formula, Types, Identities, Factor with Examples.” 2024. Testbook. Accessed June 19. https://testbook.com/maths/trinomial.