Students are asked to identify the characteristics of a quadratic function. A quadratic function is one of the form f(x) = ax2 + bx + c, where a, b, and c are numbers with a not equal to zero. The graph of a quadratic function is a curve called a parabola. This page is provided to assist a student in identifying the characteristics of a quadratic function.
Contents
Characteristics of Quadratic Functions
- The shape of a graph of a quadratic function is called a parabola which may open upward or downward and vary in “width” or “steepness”, but they all have the same basic “U” shape.
- Parabolas are symmetric about a central line called the axis of symmetry, which is always located at
x = -b/2a - The axis of symmetry intersects a parabola at only one point, called the vertex (ordered pair), which can be found using the follow expression
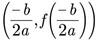
or by converting the quadratic equation into its vertex form [4] - The lowest point on the graph is the minimum
- The highest point on the graph is the maximum
- The maximum or minimum is the vertex
- The zeros (x-intercepts) can be found using the quadratic formula, or by factoring, using the square root property, or completing the square
- The y-intercept marks the point where x = 0, so substitute 0 in for x in the parabola’s equation
Look at two examples that will help you to determine the characteristics of a parabola.
Example #1

Vertex Form: f(x) = (x – 3)2 – 21
| Characteristic | Value | Characteristic | Value |
|---|---|---|---|
| vertex | (3, -21) | increasing interval | (3, +∞) |
| y-intercept | (0, -3) | decreasing interval | (-∞, 3) |
| x-intercept | x = 3 ± √(21/2) | axis of symmetry | x = 3 |
| domain | -∞ < x < +∞ | minimum value | y = -21 |
| range | y ≥ -21 | maximum value | None [2] |
| one-to-one | No [1] |
Example #2

Standard Form: (-1/2)x2 – 2x + 1
Vertex Form: y = (x + 2)2 + 3
| Characteristic | Value | Characteristic | Value |
|---|---|---|---|
| vertex | (-2, 3) | increasing interval | (-∞, -2) |
| y-intercept | (0, 1) | decreasing interval | (-2, +∞) |
| x-intercept | x = -2 ± √6 | axis of symmetry | x = -2 |
| domain | -∞ < x < +∞ | minimum value | None [3] |
| range | y ≤ 3 | maximum value | y = 3 |
| one-to-one | No [1] |
References
[1] “Vertical & Horizontal Line Test”. 2022. Mathematical Mysteries. https://mathematicalmysteries.org/vertical-horizontal-line-test/.
[2] There is no maximum value because the parabola opens up and head towards positive infinity (∞)
[3] There is no minimum value because the parabola opens down and heads towards negative infinity (-∞)
[4] The vertex form tells us how high above/below the x-axis the vertex lies (the value of k) and how far left/right of the y-axis the vertex lies (the value of h).
Additional Reading
Lloyd, Philip. “How do you find the vertex of a quadratic function by completing the square?”. 2020. Quora. https://qr.ae/pyOszL.